I_love_Hoang_Yen's blog

[GYM] 2014-2015 CT S02E10 — Solution
By I_love_Hoang_Yen, 10 years ago, In English

100534A - Abnormal Coins

This problem is the easiest amongst the problems. Since you need to choose different polygon types, the optimal way (meaning you would spend minimum amount of coins) is choosing polygon with sizes 3, 4, 5, 6, ... in this increasing order.

Code 100534B - Fake Coins

Since the length of the string is at most 1000, you can loop through all generated code. This can be done by looping through the first and second index of the code.

How to check if two code are equal? One way to do this is to use polynomial hash. For each code, you need to calculate its hash value, which can be done by using simple DP:

Let Hash(i, j) be polynomial hash of string starts at indices i and j, then:

Hash(i, j) = s(i) + Hash(j, i + j) * BASE

After calculating all the hashes, you only need to count how many different hashes are there.

Code

100534C - Coin Graph

Let f(a, b) = the length of the shortest path between a and b.

Let W(G) = total f(a, b) for all pairs of a, b.

In this type of problem, you should find a simple type of graph G, such that W(G) can be calculated easily, and from G, you can generate G' such that W(G') = W(G) + 1 or W(G') = W(G) - 1.

By trial and error, I found that Star graph has this property. A star graph with N vertices has W(G) = (N - 1)2, and you can reduce this by one simply by adding 1 edge between the 1-degree vertices. Though there are some special cases when W(G) is small, and you should handle these carefully.

Code

100534D - Coin Table

First, let's not worry about counting the number of paths. After we know how to find maximum number of coins in our path, it will be very simple to count number of paths.

Consider the following figure: We need to go from (1, 1) to (M, N), and you must not go through red cells. This will be equivalent to you must go through green cells.

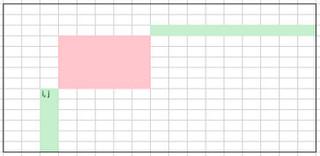
So now, to answer each query, you can loop through each green cell, and count the maximum number of coins you can have, if your path go through this cell. This can be solved using simple DP.

Code

100534E - Volleyball

This is just an implementation problem, though there are too many details, which make it very hard to code in contest time. :)

100534F - Huge Table

100534G - Coin Game

There are two possibilities: either you move all 1-coins to the left, or you move all 2-coins to the left. Let's say you want to move all 1-coins to the left. For each 1-coin, you will need to swap it with all the 2-coins that lies to the left of it. So, the total cost is the sum of (number of 2-coins to the left) for each 1-coin. This can be calculated in O(N).

Code

100534H - Dreams Were Important Too!

Let call the three edges of the triangle a, b, c.

Let p = P / 2 = (a + b + c) / 2.

Consider all values of a and b (using 2 loops :) ). Since you know P, you can calculate c. And you can check if the area of the triangle satisfies using the formula:

S = sqrt(p * (p - a) * (p - b) * (p - c).

Now, we know all the sides of the triangle. The only thing left is to find its coordinate. Obviously, you can translate the triangle, so that one vertex is at (0, 0). Let the other two vertices be (x1, y1) and (x2, y2). We know that:

a = sqrt(x1 * x1 + y1 * y1)

b = sqrt(x2 * x2 + y2 * y2)

c = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2))

To find x1, y1, x2, y2, you can generate all Pythagorean triples. Before looping through values of a and b, generate all triplets x * x + y * y = z * z where z ≤ 104.

This solution is hard to run in time. To solve it, you need to make some optimization, for example:

  • p - a must be divisor of S * S / p. This can be proven using the area formula stated above.

  • Only consider a satisfying: a < p / 2.

Code

100534I - Coin Robbery

In this problem, you are given a graph G, and you need to find the minimum number of vertex you need to 'block', so that the shortest path from 0 to N - 1 increases.

First, ignore all edges that is not on any shortest path from 0 to N - 1. Now the problem becomes, given a graph G, find minimum number of vertices to block, so that the graph is no longer connected. This can be solved using Max flow.

Code

100534J - Bimetallic coins

In this problem, you are given M = N * (N - 1) / 2 alloys. For each alloy, you know the thermal coefficient, the cost if it is inner or outer of the coin. Obviously, you can create M / 2 coins from these alloys. Now you should calculate the minimum cost. Sort the alloys in increasing order of thermal coefficient. Since you know that all the thermal coefficients are different, and an alloy with smaller thermal coefficient can only be placed outside, the problem can be solved by the following DP:

f(i, j) =  minimum cost if you considered first i alloys. There are still j alloys which are outer, but you have not find the alloy to be inner.

To calculate f(i, j), note that from a state (i, j), you can only make the following transitions:

  • Use alloy (i + 1) as outer. Then you will go to state (i + 1, j + 1).
  • Use alloy (i + 1) as inner. The outer alloy must be before (i + 1), and still not have inner alloy. So you go to state (i + 1, j - 1).

There is still one thing to take care of: when M is odd, you must ignore 1 alloy. This can be done by adding 1 more dimension to the above DP function.

Code

  • Vote: I like it
  • +47
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I found this useful for Coin Graph — http://match.pmf.kg.ac.rs/electronic_versions/Match64/n3/match64n3_639-646.pdf

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

S02E11

You mean E10, no?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Of course.. Thanks. You have very good eyes.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Well, my eyes are horribly bad, but my inner sight is that much stronger :D

      Problem H has a better solution when you set one vertex as the origin (0, 0) and the other 2 as (a, b) and (c, d). Then, A2 = ad - bc and you can, after generating all Pythagorean triples for (a, b) (around 10000 at worst), loop over all c and calculate d based on that formula. There should be very few c for which there's a valid d, and since we can consider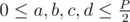 , it speeds up the code quite well.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Can someone give me test 8 of problem H please, I cant find mistake in my solution...

        → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +13 Vote: I do not like it

Does anyone have any idea about fast&easy solution for modification of J without restiction "all thermal area expansion coefficients are pairwise distinct"? I spend almost 2 hours on it:) It seems that it is possible to solve it using knapsacks for every value of C and combining them, but i have no idea how to make it run faster than M^3 in case when number of occurrences of some value is larger than M/2 (and therefore answer is less than M/2). It will be M^3 with small constant, but it still sounds bad.

P.S. I really like limitations — you have up to 1225 numbers in range 1..999, and they are all pairwise distinct:)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    。。。。I also spend 2 hours thinking the problem without the limitations. And I came up with an idea,but I don't know if it's right. I divide the pairs into groups by C, and let's think about two pair i and j. If i and j are both needed, then use i to be in and j to be out is better iff in[i]+out[j]<in[j]+out[i]. So I sort them by this to dp.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Our team didn't solve J because of this error, enabling coach mode I saw that some teams asked this question and they got a response saying 'Yes'; shall we broadcast this question for future teams?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      In the problem statement, there is sentence: "each alloy has a different thermal area expansion coefficient" (i.e. C are pairwise distinct). I am surprised that so many teams/people missed that.

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

for problem D can Someone Explain how can i get the number of ways i'm okay with the maximum number of coins but i'm stuck with the number of ways

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

D: Consider the following figure
You forgot to put the image.

Can you please explain a little about counting the number of paths?
---
Oops sorry... bad internet connection... I can now see the image.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hi I_love_Hoang_Yen I have question in problem J my code run as follow: - run Dijkstra to get the shortest path - run Dijkstra again to see if any edge get to the destination with cost > shortest_path then cancel this edge - run max flow with vertex split why this approach is wrong ?! thanks in advance 

#include <bits/stdc++.h>
using namespace std;
const int INF = 1000 * 1000 * 1000;

int n,m;

int g[105][105], cost;

int dijkstra(int source){
    vector<int > dist(105, INF);
    dist[source] = 0;
    set<pair<int, int > > q;
    q.insert(make_pair(0, source));
    while(!q.empty()){
        int current = q.begin()->second;
        int distance = q.begin()->first;
        q.erase(q.begin());
        if(current == n-1) return distance;
        for(size_t i = 0; i < n; ++i)
        {
            if(g[current][i] + distance < dist[i]){
                if(q.count(make_pair(dist[i], i))) q.erase(make_pair(dist[i], i));
                dist[i] = g[current][i] + distance;
                q.insert(make_pair(dist[i], i));
            }
        }
    }
    return dist[n-1];
}


void dijkstrA(int source){
    vector<int > dist(105, INF);
    dist[source] = 0;
    set<pair<int, int > > q;
    q.insert(make_pair(0, source));
    while(!q.empty()){
        int current = q.begin()->second;
        int distance = q.begin()->first;
        q.erase(q.begin());
        for(size_t i = 0; i < n; ++i)
        {
            //cout << distance << " " << g[current][i] << " " << current << " " << i << endl,
            if(g[current][i] + distance > cost && i == n-1) g[current][i] = INF;
            if(g[current][i] + distance < dist[i]){
                if(q.count(make_pair(dist[i], i))) q.erase(make_pair(dist[i], i));
                dist[i] = g[current][i] + distance;
                q.insert(make_pair(dist[i], i));
            }
        }
    }
}

int c[205][205];
int flow[205][205];
int bottleneck[205];
int pre[205];

void build()
{
    for(int i = 0; i < n; ++i)
    {
        for(int j = 0; j < n; ++j)
        {
            if(g[i][j] < INF) c[i*2+1][j * 2] = INF;//, cout << i << " " << j << endl;
        }
    }
}


int  maxflow(){
        int ans = 0;
        for(int i = 0; i <= 100; ++i) c[i*2][i*2+1] = 1;
        c[0][1] = INF;
        c[2*(n-1)][2*(n-1)+1] = INF;
        int S = 0, T = 2*(n-1)+1;
        while(1){
            memset(bottleneck, 0, sizeof bottleneck);
            bottleneck[0] = INF;
            queue<int > q; q.push(0);
            while(!q.empty()&&!bottleneck[T]){
                int cur = q.front(); q.pop();
                for(int i = S; i <= T; i++){
                    if(!bottleneck[i]&&c[cur][i] > flow[cur][i]){
                        q.push(i);
                        pre[i] = cur;
                        bottleneck[i] = min(bottleneck[cur], c[cur][i] - flow[cur][i]);
                    }
                }
            }
            if(bottleneck[T] == 0) break;

            for (int cur = T; cur != 0; cur = pre[cur]) {
                flow[pre[cur]][cur] += bottleneck[T];
                flow[cur][pre[cur]] -= bottleneck[T];
            }

            ans += bottleneck[T];
        }

    return ans;

}


int main()
{
    scanf("%d%d",&n,&m);
    memset(g,0x3f,sizeof g);
    for(int i = 1,a,b,c; i <= m; ++i)
    {
        scanf("%d%d%d",&a,&b,&c);
        g[a][b] = min(c,g[a][b]);
        g[b][a] = min(c,g[b][a]);
    }
    cost =  dijkstra(0);
    dijkstrA(0);
    build();
    cost = maxflow();
    if(cost == INF) cout << "IMPOSSIBLE" << endl;
    else cout << cost << endl;
    return 0;
}
→ Reply