Доброго времени суток!
Помогите, пожалуйста, решить задачу. Надо найти все простые числа на интервале N .. N+M где 1010 <= N <= 1011 и 1 <= M <= 105.
Алгоритм за O(M * sqrt(K)), где K — число, которое мы проверяем не укладывается по времени.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Доброго времени суток!
Помогите, пожалуйста, решить задачу. Надо найти все простые числа на интервале N .. N+M где 1010 <= N <= 1011 и 1 <= M <= 105.
Алгоритм за O(M * sqrt(K)), где K — число, которое мы проверяем не укладывается по времени.
| Название |
|---|



Смотри. Берешь какие-нибудь простые числа. Много простых чисел.
Например, все до 10^6.
И просеиваешь ими как в обычном решете Эратосфена свои числа от N до N+M.
Все. xD
Кстати. /blog/entry/14874.
Вроде бы, недавно был уже блог. Просто ищешь все простые числа до sqrt(N+M); Ищем за O(1000000);
как то так. А потом решетом проходишься с н до м, и убираешь числа делящие на одно из этих простых.
Блин, ответили пока код писал.
Не , по моему их болше ( ну точно болше 1000 ) ?!
Точно, затупил.
Have you tried segmented sieving method for the problem?
You can test if a number is prime with probabilistic methods as miller-rabin if i'm not wrong you can get O( it * log(n)^3 ) with it = number of iterations (with values near to 10^11 use 14) , in java is isProbablePrime with bigIntegers.
Code
Maybe this can get TLE if limit is strict as SPOJ , if this ocurrs you need to think in procesing primes <= sqrt( 10 ^ 11 ) .
And that means you only use per number.
per number.
Why don't we just use a similar algorithm with Eratosthene sieve?
Firstly, generate all of primes between 1 and 106 (actually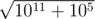 )
)
Second, create an array of bool, b[0..M]. b[i] = false if i+n hasn't been removed.
For each prime numbers in first step, try to clear all of its multipliers between N and N+M, then mark it onto array b.
This algorithm has the same complexity with Eratosthene sieve, isn't it?
Yeah you are right. Here is the code
You could use Eratosthene sieve,as some guys said. Also you can use Fermat law,which says that if p is prime then a^(p-1) MOD p = 1 1<a<p. The more a you take to test,the more sure it is that p is prime. Also to do the expontation you dont need to run it in O(N). You can use binary expontation right to left,which "break" the expontation into binary. For example if you have 5^5,because of 5=101(binary),the expontation will be 5^5=5^1+5^4.
You could use Eratosthene sieve,as some guys said. Also you can use Fermat law,which says that if p is prime then a^(p-1) MOD p = 1 1<a<p. The more a you take to test,the more sure it is that p is prime. Also to do the expontation you dont need to run it in O(N). You can use binary expontation right to left,which "break" the expontation into binary. For example if you have 5^5,because of 5=101(binary),the expontation will be 5^5=5^1+5^4.
here is wiki: http://en.wikipedia.org/wiki/Fermat_primality_test http://en.wikipedia.org/wiki/Modular_exponentiation
Мб тест Ферма поможет?
Извиняюсь за некропостинг, новый топик создавать не захотел, так как вопрос незначителен и с этой темой связан.
Может кто помочь найти задачу на КФе, где нужно строить решето Эратосфена на интервале [L, R]. Точно помню что такая была на каком-то контесте, а вот найти не смог. Также буду благодарен задачам, где используется функция Эйлера.
п.с. Задача нужна именно на КФе, чтоб её потом можно было добавить в мэшап.