Alex7's blog

Problem with data structures probably..
By Alex7, 10 years ago, In English

I've been thinking about this problem a couple of days now, and I couldn't solve it, can you please help me?

Given N companies, M sectors (sectors are adjacent and circular m is adjacent to 1) and Q queries

each query L,R, X means that sectors in the range [L,R] will get +X meteors each

Each sector is owned by a company and gets all meteors that fall in it

Each company wants to collect a certain amount of meteors.

output for each company the time when it collected the amount it wanted..(The number of the last query it required)

N<=3*10^5,M<=3*10^5, Queries <=3*10^5

  • Vote: I like it
  • +28
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 5   Vote: I like it +29 Vote: I do not like it

We're looking for every country the answer — rain number x.
To do so, we need to do parallel binsearch for all country at once, but with different intervals [left, right] for each of them.
In step one every country c has left[c] = 0, right[c] = k. (k-th rain has infinity amount of meteors)
In every step we iterate over each rain, add its interval to segment tree. Also we keep vector<int> check[k]. check[i] stores all countries, that we need check how many meteors lands on their segments after i-th rain. We can make it with segment tree in O(logm).
If country c is 'satisfied' we change right[c] = i, otherwise left[c] = i + 1. If left[c] < right[c] we add country c to check[(left[c]+right[c])/2].

We keep doing this until all check[i] are empty.

Complexity:

while(changed) { // up to O(logk)
        REP(i, k) { // O(k)
            rain_go(i); // O(logm)
            while(check[i].size()) {
                int c = check[i].back(); check[i].pop_back(); // c - current country
                ll curval = 0; // sums of meteors on country's sectors after i rains
                REP(j, sectors[c].size()) curval += tree.query(sectors[c][j]); // amortized O(mlogm), every sector at most 1 time
                if(curval >= p[c]) right[c] = i;
                else left[c] = i+1;
                if(left[c] < right[c]) {
                    check[(left[c] + right[c] )/2].pb(c);
                    changed = true;
                }
            }
        }
    }

O((m + k)log(k)log(m))

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I coded your idea and it runs much faster than I expected.. something like ~5 seconds while the time limit is 35 seconds for the biggest test case...

    And I have to say it's one of the most beautiful ideas in programming that I've encountered :D :D

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you provide your implementation?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Here

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I have a question. I read flashion's comment and read your code. When I read the problem I had a different interpretation of the problem. I now realized that I am wrong but I think my interpretation is interesting (and more difficult?)

          Suppose a state controls sector 1 and 2. Suppose a meteor shower (with 5 meteors) happen at sector 1 and 2. Then the state gets 10 meteors according to the problem. When I read it, I interpreted that the state should get 5 meteors since well, they are the same meteors.

          Thus, suppose I change the problem to: if a meteor shower with A meteors happens in sectors in range [L,R], and a state controls at least one sector in [L,R], then the state gets A meteor samples. How should this be solved? I think a segment tree (at least a normal one) does not work here.

          → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    @flashion

    great idea !! understood the idea completely but not able to verify complexity of this solution it is amortized (I know what does it mean ) but even then i am not getting this .. Please help

    → Reply
»
10 years ago, # |
← Rev. 10   Vote: I like it +16 Vote: I do not like it

I think you can solve this problem with persistent segment trees too. You apply all the updates and then for each country you just binary search over the time(answer for the country) using the segment tree. Complexity: mlogmlogn When I saw that companies owning the states, I thought my solution wouldnt work but it works. Here is my implementation: http://mirror.codeforces.com/contest/493/submission/9022316 (It gets mle, need a memory limit of 256mb)

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

You also can use sqrt-decompositon to solve this problem.

code

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone familiar with main.edu.pl please tell why I am getting 98/100 points (13/15 points for 7th test group), even though my solution passed all the tests (all OK)?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Lol, I had a similar feedback in a different problem.. I think they subtract a few points when your solution is relatively slow...

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +6 Vote: I do not like it

    100% points for test, <= 1/2 limit
    0-100% points (linear), <1/2, 1> limit
    0% points for group of tests, at least one test > time limit

    There's a taks from Polish Olympiad. You can get from 0 to 100 points for one task there. The real time limit (to get 100%) is half of the visible in Main.

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

The obvious solution that comes to mind is persistent segment tree with complexity O(X * logM * logQ) for each country, where X is the number of sectors owned by that country. Since each sector is owned by only one country, the total complexity would be O(M * logM * logQ), which should be fast enough, though I'd need to test it to be sure.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is fast enough, IMHO. But memory is limited to 64 MB :(

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it +3 Vote: I do not like it

      Mmmhhhh, that's a problem indeed. It wouldn't fit in memory, so I solved it with sqrt-decomposition. My solution is not fast enough to get 100 points though...

      Nice problem anyway!

      C++ code

      EDIT: I changed the block size from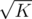 to a fixed size of 1200 and now it works much faster.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        I just implemented tom's approach and it got 100. His idea is really a nice way-around with the memory limit :) In essence,the solution with persistence and "parallel binary search" is same — both does binary search to find the answer. But, the later one can be utilized anywhere with a strict memory limit :)

        I always liked Polish Informatics Olympiad problems :D I with there were some sort of editorial ( although I should not complain much. We can always ask here in CF )

        → Reply