Hi, everybody.
I'm interested in how to solve the next problem 18.
It's obvious, that if 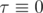 curve is plane.
curve is plane.
Transform torsion at point ρ(s) as 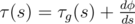 , where
, where 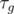 — is geodesic torsion at the point, and φ is angle between osculating plane and tangent plane.
— is geodesic torsion at the point, and φ is angle between osculating plane and tangent plane. 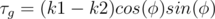 , where k1 and k2 are principal curvatures.
, where k1 and k2 are principal curvatures.
Also, if we consider the case, when curve doesn't lay in plane, and surface is a sphere. At any point on sphere k1(s) = k2(s), and we have to prove that 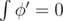 .
.
In other cases we are able to find a point, where k1 ≠ k2. And I guess we should constract such curve in a neighbourhood of that point 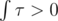 .
.
Any ideas how to complete this solution? Or any others solutions are welcome.
UPD1 Solution for sphere.
Let 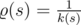 . If the curve lays on the sphere then the equality
. If the curve lays on the sphere then the equality 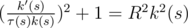 holds. By means of a little transformation of this equality, we can obtain
holds. By means of a little transformation of this equality, we can obtain 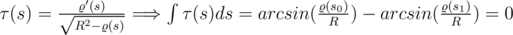 .
. 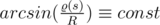 , because the radius of curvature is constannt in any point on the sphere.
, because the radius of curvature is constannt in any point on the sphere.











You should've start with:
"I solved first 17 problems and got 2147 rating, but I can't solve 18'th, help me, I want to be red"
that's the only way to make everyone willing to help