Всем привет!
Недавно на тренировочных сборах MIPT: The Fall на контесте от Александра Milanin была задача с Petr Mitrichev Contest 7. Суть её заключалась в том, что нам был дан граф и множество запросов вида "допустим, мы удалили из графа k ≤ 4 рёбер. Остался ли он связным?" Я не знаю, какое решение предполагалось автором (буду благодарен, если кто-то расскажет или скажет, где его можно найти, говорят, там что-то красивое :), но далее я хочу рассказать о решении более общей задачи, когда рёбра произвольно добавляются и удаляются, за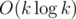 
в оффлайне. Первый алгоритм с такой оценкой был получен Дэвидом Эппштейном в 1992 году сведением к fully dynamic minimum spanning tree problem, однако здесь речь пойдёт о более простом алгоритме, предложенном в 2012 году Сергеем Burunduk1 Копелиовичем.
Будем считать, что запросы бывают трёх типов — добавить ребро (+), удалить ребро (-) и узнать некоторую информацию о графе (?) (в данном случае пусть это будет число компонент связностей графа). Будем считать, что нам на вход поступило k запросов. Рассмотрим k + 1 моментов времени — начальный и k моментов после каждого из запросов. Для удобства преобразуем запросы первого вида в запросы вида "ребро i присутствует в графе с момента времени l по момент времени r" (!).
Итак, пусть у нас есть граф G = < V, E > и набор запросов к нему. Пусть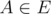 
— множество рёбер, которые постоянно присутствуют в нём (т.е. были изначально и не было запросов на их удаление). Сожмём каждую компоненту связности, образованную такими рёбрами в одну вершину и построим новый граф на этих вершинах. Кроме того выкинем все вершины, которые не упоминаются в списке запросов (чтобы работать с графом из k вершин). Переделаем запросы таким образом, что если в начальном графе запрос был обращён к паре вершин (a, b), то теперь он будет обращён к паре вершин-компонент связностей (comp(a), comp(b)).Видно, что выполнение ?-запросов на новом графе будет иметь абсолютно такой же результат, что и на начальном. Далее предлагается такой алгоритм: поделим обрабатываемый в данный момент промежуток времени пополам и рекурсивно разрешим сначала левую, а затем правую части и таким образом получим ответы для всего набора запросов. База — единичный момент времени, обрабатывается тривиально — в этот момент нам на вход подаётся граф без рёбер, следовательно, для любого запроса ответом будет число вершин в этом графе. При этом на каждом шаге, обрабатывая подотрезок запросов [l;r), будем хранить только те вершины, которые упоминаются на этом подотрезке, тогда запрос [l;r) будет обработан за O(r - l), что даст 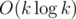в сумме по всем подотрезкам.
Теперь о технической части реализации. Можно делать это именно так, как описано в условии, а можно слегка упростить решение, воспользовавшись СНМ (впрочем, тогда в ассимптотике выскочит лишний логарифм). Будем объединять компоненты связности в одну вершину, сливая её в одно множество в СНМ. При запросе к подотрезку [l;m) нам потребуется добавить в СНМ рёбра, которые были добавлены раньше него и которые мы впервые (в рамках подотрезка [l;r)) удаляем в подотрезке [m;r), а при запросе к подотрезку [m;r) нам соответственно надо будет удалить добавленные на прошлом шаге (это можно сделать обычными откатами структуры), но зато добавить те, которые мы добавляем в [l;m) и не удаляем в [m;r). И то, и то легко делается за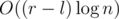 
в пару проходов по отрезку. Перед выходом из отрезка также нужно подчистить за собой все сделанные изменения, чтобы не влиять на возможную обработку последующих отрезков. Итоговая ассимптотика 
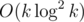. Стоит отметить, что существует реализация СНМ, дающая оценку 
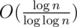на запрос, что позволяет опустить теоретическую планку до 
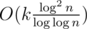, впрочем, это уже мало применимо на практике :)
Также Сергеем был предложен похожий по идее алгоритм поддержания компонент двусвязности (а также мостов) в динамически меняющемся графе за 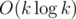в оффлайне. О нём можно прочесть в его дипломе, который приложен ниже.
Подводя итог, хотелось бы традиционно предложить решить несколько задач по теме. Специально для этого была сделана тренировка на кф, в которую добавлены задачи, которые в своё время Сергей давал на различных соревнованиях, а также уже упомянутая задача с Petr Mitrichev Contest. Good Luck & Have Fun!
P.S. Подробнее о структуре и прочих алгоритмах решения задачи (а также о доказательстве некоторых тривиальных фактов, которые были опущены) можно почитать в дипломной работе Burunduk1.
adamant выпилили из топ-10?)
Сколько можно этим его троллить? Тем более пост стоит плюса, хотя бы за ссылку на дипломную работу. Кроме шуток, это вообще первая дипломная работа, которую я вижу в глаза — а самому еще писать (кстати, там рядом их полно лежит). Ну и еще теперь я вижу, что даже такой яркий лектор, как Burunduk1 может плохо подготовиться [youtube] . Очень хотелось больше картинок) А уж комментарии KOTEHOK и отзыв andrewzta (только сейчас досмотрел) интересны были бы даже по отдельности.
UPD наткнулся на работу с названием "Моделирование одежды в реальном времени", убило) По содержанию работа как работа, но название)
Почему с СНМ выскакивает лишний логарифм?
т.к. приходится использовать снм с откатами, а это не позволяет пользоваться эвристикой сжатия пути. Таким образом снм начинает работать за Log.
Одно из известных решений — использование cut space/cycle space графа; ниже очень примерное описание.
Рассмотрим векторное пространство над
, где каждая координата вектора соответствует ребру графа. Каждый вектор можно рассматривать как подмножество ребер, сумму — как симметрическую разность.
Цикловое пространство — подпространство описанного выше пространства, порожденное всеми циклами графа; пространство разрезов — подпространство, порожденное всеми разрезами (а на самом деле, состоящее из разрезов, потому что сумма разрезов — тоже разрез). Про них интересно следующее: все элементы циклового пространства перпендикулярны всем разрезам;
более того, прямая сумма этих двух подпространств образует все пространство (доказать предлагаю самостоятельно).Пусть мы хотим проверить, является ли данное множество ребер разрезом. Из написанного выше следует, это эквивалентно тому, что это множество (как вектор) перпендикулярно всем элементам циклового пространства. Можно было бы сделать так: выбрать много случайных элементов cycle space и проверить перпендикулярность, но это слишком долго.
Введем базис в cycle space следующим образом: выберем любое остовное дерево, в нем между любыми двумя вершинами единственный путь. Сопоставим каждому ребру, не лежащему в дереве, цикл, состоящий из этого ребра и пути в дереве. Все такие циклы образуют базис в cycle space.
Сопоставим каждому такому элементу случайный бит, получили случайный элемент cycle space; теперь скалярное произведение каждого из ребер с данным элементом вычисляется динамикой по дереву. Чтобы получить скалярное произведение для произвольного множества, сложим посчитанные величины для всех ребер. Чтобы производить сразу много проверок, будем каждому элементу сопоставлять не один бит, а 64, и складывать их в int64.
Проверять разрез научились. После удаления множества ребер граф становится несвязным, если в этом множестве хотя бы одно подмножество — разрез. В итоге получили решение за O(n + m2k)
"прямая сумма этих двух подпространств образует все пространство" — к сожалению, у нас пространство не Евклидово (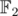
— не самое хорошее поле), поэтому это неверно. Хоть подпространства и ортогональны, но они нетривиально пересекаются.
Хм, и правда. Забавно, сообществу потребовалось два года, чтобы найти эту ошибку :)
Пример: в K4 любой цикл длины 4 является также разрезом вида K2, 2.
Да, спасибо, убрал эту фразу.
Я тебе говорю, в первой реализации не нужна очередь ребер, просто ребра из парного вызова в рекурсии.
Nice problem. I thought about a somewhat different solution for the offline problem, which seems a bit easier to me, from a conceptual point of view. Let's construct a segment tree over the k time moments. Then, each operation of type "edge i is available from time L to time R" is inserted in the O(log(k)) segment tree nodes which cover the interval [L,R]. This step takes O(k*log(k)) time and memory.
Then we traverse the segment tree by using DFS starting from the root. During the traversal we maintain the connected components of the graph using disjoint sets. When we enter a segment tree node, we perform a Union operation for each edge which is stored in that node. We also store the successful Union operations in a stack of operations so that, when we exit a segment tree node, we are able to undo all the Union operations performed when entering the node. Before exiting a leaf node of the segment tree node which corresponds to a "?" operation we have the answer as the number of sets in the disjoint sets data structure (which we maintain as a separate variable which is updated when a Union is successful and when a Union is undone).
If we use only union by rank or union by size for the disjoint sets the overall time complexity is O(k*log^2(k)). If we also use path compression then the time complexity should be lower, but I don't know how to compute how low it would go (i.e. I'm not sure if it would become O(k*log(k)*alpha(k)) or something else, where alpha is the inverse Ackermann function).
Hi
That seems easier to me too. But can you elaborate the approach to undo all the operation done while traversing the segment tree?
Here is what I am doing while traversing the tree. I am adding all the edges present on the segment tree node using disjoint-union data structure (which changes the representative array of disjoint union data structure). To do these operations I need to copy the representative array into another array. Considering segment tree can have 4*(3*10^5) nodes and the graph we are considering can have 3*10^5 nodes the above operation will surely TLE.
Can you help me to reduce the time complexity here?
Thanks :D
Correct me if I'm wrong, but I think "segment tree" is an incorrect translation and the actual term is "interval tree" (at least according to this thread)
that is "segment tree"中文线段树,no problem.
I don't think you can very easily optimize a DSU data structure with path compression to support undo operations (without writing all the path compressions to memory). Moreover, I highly doubt the "true" complexity will be O(α(n)), as undo operations tend to break all algorithms that relied on amortized operations. I really wonder how the author's proposed algorithm truely is O(klog(k)).
There is a provable O(klogk) solution to the offline dynamic connectivity problem, but with a larger constant factor. The key idea is to use link-cut tree to maintain the maximal spanning tree where the weight of edges are their deletion time. With a piece of link-cut tree code, it's fairly easy to implement.
code: link
You can also use link-cut trees for dynamic bridges (problem D) in
. It tricky to implement, but faster in practice than the divide&conquer+dfs solution.
А правда ли, что первой реализацией нельзя отвечать на запросы о том, лежат ли две вершины в одной компоненте связности быстрее чем за O(klog2k)? Все что я придумал — это держать текущую покраску для O(logk) слоев рекурсии, и когда мы обрабатываем граф без ребер — спускаться по этой покраске и смотреть, правда ли, что интересующие нас вершины имеют один и тот же цвет. Если да — ответ на запрос положительный, иначе делаем что-то вроде
и продолжаем искать.
Вроде бы можно дополнительно передавать в рекурсию список get-запросов текщуего отрезка и на нем делать аналогичные преобразования за O(r - l). Тогда суммарно таки выйдет O(klogk)
Is there an English version of the diploma available anywhere?
there is a mistake in the statement of problem b. 1 ≤ M ≤ 10^5, but the M in the sample test is 0. maybe 0 ≤ M ≤ 10^5 ? :)
can we use disjoint sets with sqrt decomposition for this problem ?? a solution of similar problem (disjoint set union division) is given in this site http://e-maxx.ru/algo/sqrt_decomposition but i didn't understand this completely
Can anybody give link to a problem "just implement DCP-offline"?
100551A - Connect and Disconnect
Is there anyway to get the actual test case content for 100551A — Connect and Disconnect? I can't figure out why I keep getting a runtime error, even if the sample case works just fine; seems to be some memory issue, but it's quite frustrating.
Did u remember to read/write to input/output files, becos this question requires u to do that.
...that's true, thanks a lot Ryan, completely forgot about that. Kudos for the fast response!
Ur welcome :)
Is it legal to cast pointer to int. (In log2 implementation)? I don't think it is right, but it passes everywhere I submit this version of DSU.
1303F is another example.
It seems like it's very hard to get dynamic connectivity to pass for that problem.
https://mirror.codeforces.com/blog/entry/73812?#comment-580151
https://mirror.codeforces.com/blog/entry/73812?#comment-580000
Here's a slightly more code-heavy solution that I haven't seen anyone explain yet:
Suppose we want to sweep through the time steps and maintain a maximum spanning tree of the currently alive edges. When we hit a new edge e=(u->v) that we want to process, we have to find the first edge that gets deleted on the path from u to v. If that edge gets deleted before e, we should remove that edge from our MST and replace it with e. Otherwise, all edges in that path are better than e, so we should just ignore that we tried to add e. When we get to a time that we have to delete and edge, if it is in the MST, we simply delete it from the MST. Otherwise, we skip the query.
Clearly, all that matters in this situation is whether two nodes are connected in the MST: if they are, then they would be in the graph. If they aren't connected in the MST, then they aren't connected in the graph either; if there was some edge that got deleted later than now, then by definition, it would be in the MST right now.
All that is left is finding the latest-deleted edge along a path in some data structure that supports adding and deleting edges. We can do this with a link cut tree fairly easily by conceptually splitting each edge into two edges and one node of degree 2. For instance edge e=u->v would look like [u — e — u] where e is the node in the LCT that represents its corresponding edge.
Can someone please explain this in more detail for me? It seems like a divide-and-conquer over time but the explanation of how the problem is actually divided is missing.
Edit: I figured it out. The part where the always connected components are collapsed is done for every recursive call, not just once at the beginning.
The last problem Disconnected Graph might have another solution in $$$O(K2^c)$$$。
After building the dfs tree of the graph, we can assign a random value to every non-dfs-tree-edge, and define the value of each dfs-tree-edge as the XOR of the values of all the non-dfs-tree-edges which cover it. Then, when querying each small set of $$$c$$$
edges, we can $$$O(2^c)$$$ check each subset of the set and see if the XOR of the edges are $$$0$$$. If it is, then we can almost claim that after deleting this subset the graph will be disconnected.