Can anyone please tell me the process how to solve this problem . Thanx in advance :)
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.11.2024 15:21:10 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Fix two rows and consider all cells between them as an single array... From left to right count for each position the subarrays ending in it, that subarray sum is between A and B, this can be done in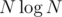
for fixed rows (with a binary indexed tree), and overall time 
...
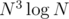... which will probably not fit in the time limit. You should remember about two pointers method when you come up with a binary search solution — perhaps it would make the solution faster.
you are right, but my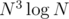
pass in time... but i have to recognize than two pointer method is even better...
can you explain how to use that BIT ? Thanks!
we are going to solve the problem with 1D array L = {x1, x2, ..., xn}, let be si = x1 + x2 + ... + xn, and s0 = 0. process L from left to right, if we have an structure that allow us to know how many elements are in range [a, b] when we process xi, if it is the last element in a subarray whose sum is in [a, b], then exists sj(j < i) such that a ≤ si - sj ≤ b, or the same si - b ≤ sj ≤ si - a, then we can add to our solution how many sj are in this range, and add si to the structure for future queries. We can use a treap, but if we process and compress in advance all si, we can use a BIT and the implementation would be easier.
Your text to link here...