Fear_Is_An_Illusion's blog

Math Problem. Need Help
By Fear_Is_An_Illusion, 10 years ago, In English

Hello everyone. I had doubts solving this problem. Since problem statement isnt that long, I decided to include it.

Nikhilesh loves factorials. One day he was working on exponents and starts wondering what would be the exponent of a number in the factorial of another number. He defines a function Exp(N,k) as:

Exp(N,k) = largest Y such that kY is a factor of N! .

He calculates Exp(N,k) for all values of k from 2 to N .

Since he is bad at remembering numbers, he computes the sum of Exp(N,k) for all k in range [2,N]. This sum is easy to remember.

Your task is to calculate this sum for a given value of N. Since the value can be large, print its modulus with mod (ans%mod).

I used miller rabin primarility test for generating primes. Then I factorised every number upto N, stored it in a place. Then I found out the frequency of each element and stored it along with that element in a pair. So I had all the prime factors and exponents of the factorial, which I used to solve the question.

However this is extremely slow for large input.

Any other feasible method ?

Thanks for help.

Link To Problem

  • Vote: I like it
  • -4
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Exp(N,k) = largest Y such that kY is a factor of N! .

Did you mean k^Y?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It's k^Y in the problem statement (hackerrank).

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Any link to the problem statements in hackerrank?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Read topic carefully.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thanks. I am not used to the hyperlink with no underline. :-p

          → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

Method is essentially the same: you factorize every number from 1 to N and do some calculations with frequencies.

However, N = 107 hints us, that factorization is rather slow. Therefore, one should use sieve of Eratosthenes to precalculate smallest\largest prime, that divides every number. Here is a pseudocode (which I used during contest): 

int largest[N]
fill 'largest' with zeroes
largest[1] = 1
for i in [2..N]:
  if largest[i] == 0: // 'i' is a prime number
    for j in [i:N] with step i:
      largest[j] = i;

Sieve works in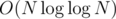 or something like that. You can find out more about it on wikipedia.

The last part of solution is factorizing number, given an array 'largest'. It goes like this: 

function factorize(n):
  factors = list()
  while n > 1:
    int factor = largest[n]
    n /= factor
    factors.add(factor)
  return factors

This method iterates on n's factors directly, so it works in p1 + p2 + ... + pk moves, given that n = a1p1a2p2... akpk

→ Reply