Мы хотели бы также поблагодарить тестеров задач этого раунда и олимпиады ЗКШ: alger95, thefacetakt, adamant, -imc-, riskingh, ASverdlov.
Пожалуйста, пишите в комментариях о найденных ошибках.
UPD: я вспомнил, что забыл написать регулярные бонусные челленджи. Так что вот, пожалуйста.
Идея:Endagorion
Подготовка:Endagorion
Чтобы проверить, что все буквы присутствуют, заведем массив длины 26 и для каждой буквы поставим в соответствующую ячейку единичку. В конце надо проверить, что все 26 единичек на месте. Решение работает за O(n). Также надо не забыть перевести все буквы к нижнему регистру (или наоборот, все буквы к верхнему).
Чтобы перевести буквы в нижний регистр, можно использовать встроенные функции, например, tolower в Python. Также можно пользоваться тем, что буквы от a до z идут подряд по их ASCII-номерам; ASCII-номер для символа можно получить при помощи ord(c) во многих языках. Теперь, чтобы получить номер буквы в алфавите, надо написать ord(c) - ord('a'), а на C++ или C просто c - 'a' (поскольку в C/C++ символ — это число, равное его ASCII-номеру). Также, например, чтобы проверить, что буква имеет нижний регистр, надо написать неравенство ord('a') <= ord(c) && ord(c) <= ord('z').
Challenge: сколько существует различных панграмм длины n? Строки, отличающиеся капитализацией некоторых символов, считаются различными. Сможете ли вы придумать линейное по времени решение?
Идея: Endagorion
Подготовка: Endagorion
Самое простое решение — просто запустить обход в ширину. Построим граф, в котором вершины — числа, а ребра ведут из одного числа в другое, если можно получить второе из первого за одну операцию. Можно заметить, что первое число никогда не выгодно делать больше, чем 2m, поэтому в графе будет не больше 2·104 вершин и 4·104 ребер, и BFS сработает очень быстро.
Однако, есть решение гораздо быстрее. Развернем задачу: изначально у нас есть число m, и мы хотим получить число n, пользуясь операциями "прибавить к числу 1" и "поделить число на 2, если оно четно".
Пускай мы в какой-то момент применили две операции типа 1, и потом операцию типа 2; но эти три операции можно заменить на две: сначала операция типа 2, а потом одна операция типа 1, и количество операций от этого уменьшится. Отсюда следует, что применять больше одной операции типа 1 имеет смысл только тогда, когда операций типа 2 больше не будет, то есть, когда n меньше m и осталось сделать несколько прибавлений, чтобы их сравнять. На самом деле, теперь существует ровно одна последовательность операций, удовлетворяющая таким требованиям: если n меньше m, прибавляем единички пока нужно, иначе если n четно, делим на 2, а если нечетно, прибавляем 1 и потом делим на 2. Количество операций в такой последовательности можно найти за время  .
.
Challenge: рассмотрим обобщенную задачу: мы хотим получить число n из числа m с помощью операций двух типов "отнять a" и "умножить на b". Обобщите решение исходной задачи и научитесь находить минимальное количество операций за время  в случае, если a и b взаимно просты. Справитесь ли вы, если у a и b могут быть нетривиальные общие делители?
в случае, если a и b взаимно просты. Справитесь ли вы, если у a и b могут быть нетривиальные общие делители?
520C - Выравнивание ДНК/521A - Выравнивание ДНК
Идея: Endagorion
Подготовка: Endagorion
Что это за функция — ρ(s, t)? Для каждого символа t и каждого символа s существует ровно один циклический сдвиг, который их совмещает (действительно, после 0, ..., n - 1 сдвигов символ t пробежит все возможные положения в строке, и ровно одно из них — это положение символа из s); поэтому, существует ровно n способов циклически сдвинуть s и t, при которых выбранные символы совместятся (поскольку ситуация симметрична для любого положения символа из s). Таким образом, вклад в ρ, который дает символ ti, равен n × (количество символов s, равных ti). Поэтому ρ(s, t) максимально, когда каждый символ t встречается в s наибольшее количество раз. Посчитаем для каждого символа количество вхождений в s; ответ равен Kn, где K — это количество типов символов, которые встречаются в s чаще всего. Решение за O(n).
Challenge: мы знаем, что ρmax(s) = C(s)·n2, где C(s)--- максимальное количество вхождений какого-либо символа. Сколько существует строк s длины n над алфавитом размера k, таких что C(s) = m? Сможете придумать решение за время O(kn2)? За время 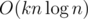 ? За время
? За время 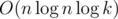 ? Может быть, еще быстрее? (Подсказка: для быстрого решения необходим удачно подобранный простой модуль. =))
? Может быть, еще быстрее? (Подсказка: для быстрого решения необходим удачно подобранный простой модуль. =))
Идея: savinov
Подготовка: savinov, sokian, zemen
В эквивалентной формулировке, первый игрок стремится максимизировать лексикографиский порядок последовательности кубиков, а второй игрок — минимизировать его. Поэтому, на каждом шагу первый игрок берет максимальный из доступных кубиков, а второй — минимальный.
Сперва научимся проверять, можно ли в текущей ситуации взять некоторый кубик. Его нельзя взять только тогда, когда есть какой-то кубик, который на нем "стоит" (т.е. имеет координаты (x - 1, y + 1), (x, y + 1) или (x + 1, y + 1)), и наш кубик является единственным, на котором он стоит. Это условие можно явно проверить. Из-за больших координат это не получится сделать путем простых обращений к массиву, поэтому придется завести ассоциативный массив, например, в C++ можно воспользоваться set.
Теперь надо научиться находить максимальный/минимальный кубик среди доступных. Просто линейный проход — это слишком долго, поэтому заведем еще одну структуру, в которой будем хранить номера доступных кубиков. Структура должна уметь добавлять, удалять, а также искать максимум/минимум, так что что-нибудь вроде set нам снова подойдет.
После того, как ход сделан, какие-то кубики могли стать доступными или, наоборот, перестать быть доступными. Однако, после каждого хода состояние могло поменяться только для O(1) кубиков: кубики (x ± 1, y) и (x ± 2, y) могли стать недоступными, потому что какой-то из кубиков выше стал опасным (т.е., остался один кубик, на котором он держится), и еще какие-то из кубиков (x - 1, y - 1), (x, y - 1) и (x + 1, y - 1) могли сделаться доступными, потому что единственный опасный кубик, который на них стоял, был удален. В любом случае, для всех них надо просто заново сделать проверку, и про случаи можно особо не думать.
Решение с подходящей структурой работает за  .
.
Challenge (по мотивам вопросов от jk_qq и RetiredAmrMahmoud): пусть теперь кубики выкладываются в ряд справа налево, т.е. от младших разрядов к старшим. Первый игрок все так же хочет максимизировать итоговое число, второй — минимизировать его. Если оставить правила убирания кубиков такими же, в общем случае задача не выглядит решаемой. Попробуйте решить новую задачу в случае, когда кубики выстроены в несколько независимых башен, т.е. кубик можно убрать, если он находится на вершине своей башни.
520E - Сплошные плюсы/521C - Сплошные плюсы
Идея: Endagorion
Подготовка: gchebanov, DPR-pavlin
Рассмотрим какой-нибудь способ расставить плюсы, а также какую-то цифру di (цифры пронумеруем с нуля слева направо). Эта цифра дает вклад в сумму чисел, равный di·10l, где l — расстояние до ближайшего плюса справа или до конца строки, если справа нет плюсов. Если просуммировать эти значения по всем цифрам и по всем способам расставить плюсы, получим в точности ответ.
Сколько существует способов расставить плюсы для выбранной цифры di и какого-то фиксированного l? Во-первых, рассмотрим случай, когда при разбиении по плюсам часть, содержащая цифру di, не является последней, т.е., i + l < n - 1. Всего существует n - 1 позиция, куда можно ставить плюсы; ограничение, связанное с цифрой di и расстоянием l, означает, что после цифр di, ..., di + l - 1 плюсов не стоит, а после цифры di + l плюс стоит. Иными словами, строка выглядит примерно так:
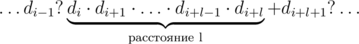
На рисунке точка означает отсутствие плюса, а вопросик значит, что неважно, стоит там плюс или нет. Видно, что из n - 1 возможных позиций для плюсов состояния (l + 1)-ой позиции определены, и среди них использован только один плюс. Это значит, что в остальные (n - 1) - (l + 1) = n - l - 2 надо поставить k - 1 плюс любым из способов; значит, искомое количество способов равно 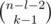 . Рассуждая схожим образом, получим, что если цифра di входит в последнюю часть (т.е. i + l = n - 1), количество способов равно
. Рассуждая схожим образом, получим, что если цифра di входит в последнюю часть (т.е. i + l = n - 1), количество способов равно 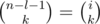 .
.
В итоге получаем, что ответ равен
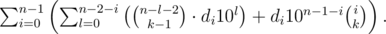
Преобразуем:
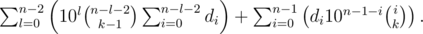
Чтобы посчитать такие суммы, нам надо предпосчитать все степени 10 до n-ой (по модулю 109 + 7), а также биномиальные коэффициенты. Чтобы их посчитать, вспомним, что 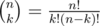 , поэтому достаточно вычислить все k! для k вплоть до n, а также их обратные значения по модулю. Помимо этого, нам пригодится массив префиксных сумм для цифр di, т.е., значения
, поэтому достаточно вычислить все k! для k вплоть до n, а также их обратные значения по модулю. Помимо этого, нам пригодится массив префиксных сумм для цифр di, т.е., значения 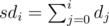 . Осталось просто просуммировать произведения этих величин.
. Осталось просто просуммировать произведения этих величин.
В итоге получили решение за 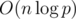 , поскольку стандартные алгоритмы для поиска обратных по модулю (а именно, малая теорема Ферма с бинарным возведением в степень и решение диофантова уравнения при помощи обобщенного алгоритма Евклида) имеют верхнюю оценку сложности
, поскольку стандартные алгоритмы для поиска обратных по модулю (а именно, малая теорема Ферма с бинарным возведением в степень и решение диофантова уравнения при помощи обобщенного алгоритма Евклида) имеют верхнюю оценку сложности 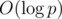 . Однако, можно воспользоваться интересным трюком и вычислить все обратные элементы для первых n чисел за линейное время, после чего итоговоая сложность решения становится O(n); почитать про интересный трюк можно в комментарии от Kaban-5 (непонятно, почему он заминусован; может быть, кто-то вспомнит ссылку на более фундаментальный источник для этого метода?).
. Однако, можно воспользоваться интересным трюком и вычислить все обратные элементы для первых n чисел за линейное время, после чего итоговоая сложность решения становится O(n); почитать про интересный трюк можно в комментарии от Kaban-5 (непонятно, почему он заминусован; может быть, кто-то вспомнит ссылку на более фундаментальный источник для этого метода?).
Challenge: теперь мы хотим посчитать сумму всех выражений, в которых расставлено k плюсов для всех k от a до b; т.е. мы хотим просуммировать ответы для исходной задачи по всем k = a, ..., b. Числа a и b любые, такие что 0 ≤ a ≤ b ≤ n - 1. Решение за O(n2) очевидно: для каждого k посчитаем ответ отдельно. Сможете ли вы придумать решение за линейное время?
Идея: Endagorion
Подготовка: gchebanov
Пусть у нас есть только умножения. Тогда нам даже не важно, в каком порядке их применять, надо просто брать несколько апгрейдов с максимальным bi.
Теперь рассмотрим также прибавления, а про умножения временно забудем. Ясно, что для каждого скилла надо взять несколько максимальных прибавлений (возможно, ни одного). Для каждого скилла отсортируем прибавления по невозрастанию bi; теперь для каждого скилла надо взять несколько первых апгрейдов. Итак, теперь для выбранного скилла есть невозрастающая последовательность прибавлений b1, ..., bl, и начальное значение скилла равно какому-то a. Раз мы решили взять некоторый префикс массива b, это значит, что когда мы берем апгрейд bi, значение скилла увеличивается с a + b1 + ... + bi - 1 до a + b1 + ... + bi - 1 + bi. Иными словами, значение, на которое домножится значение скилла (а значит, и все произвдение значений скиллов), равно дроби 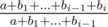 . Теперь, когда это отношение однозначно определилось для каждого прибавления, мы можем считать любое прибавление умножением. =) Теперь посчитаем такие отношения для всех прибавлений (т.е., отсортируем b-шки для каждого скилла по отдельности и найдем значения всех дробей), и затем посортируем умножения и прибавления вместе по тому, во сколько раз они увеличивают итоговый ответ. Ясно, что все умножения надо использовать уже после того, как были сделаны все прибавления; иными словами, для определения того, какие апгрейды брать, мы сортируем их все вместе по их отношениям, но реальный порядок применения должен быть таким: сперва все прибавления, а потом все умножения.
. Теперь, когда это отношение однозначно определилось для каждого прибавления, мы можем считать любое прибавление умножением. =) Теперь посчитаем такие отношения для всех прибавлений (т.е., отсортируем b-шки для каждого скилла по отдельности и найдем значения всех дробей), и затем посортируем умножения и прибавления вместе по тому, во сколько раз они увеличивают итоговый ответ. Ясно, что все умножения надо использовать уже после того, как были сделаны все прибавления; иными словами, для определения того, какие апгрейды брать, мы сортируем их все вместе по их отношениям, но реальный порядок применения должен быть таким: сперва все прибавления, а потом все умножения.
Наконец, разберемся с присваиваниями. Очевидно, что для каждого скилла имеет смысл делать не более одного присваивания, и использовать можно только максимальное присваивание для данного скилла. Кроме того, присваивание необходимо делать перед всеми прибавлениями и умножениями. Поэтому, для каждого скилла надо просто определиться, берем мы для него максимальное присваивание или нет. Однако есть проблема с тем, что когда мы сделали присваивание, отношения для прибавлений стали неправильными, поскольку стартовое значение a поменялось.
Представим теперь, что мы уже выбрали, какие прибавления мы сделаем, и теперь решаем, брать присваивание или нет. Если мы берем присваивание, то итоговое значение скилла поменяется с a + b1 + ... + bk на b + b1 + ... + bk. Иными словами, присваивание работает примерно так же, как и прибавление значения b - a. Единственная разница в том, что присваивание необходимо ставить раньше всех прибавлений.
Итак, переделаем все максимальные присваивания для каждого скилла в прибавления b - a и обработаем их вместе со всеми остальными присваиваниями (которые, как мы знаем, в итоге станут умножениями =)).
В итоге, задача свелась к сортировке отношений для всех апгрейдов. Оценим, какие числа у нас будут стоять в дробях. Отношение для умножения — это целое число до 106; отношение для прибавления — это дробь, которая выглядит как 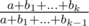 . Поскольку k может быть порядка 105, а bi — порядка 106, числитель и знаменатель дроби могут быть порядка 1011. Когда мы сравниваем дроби
. Поскольку k может быть порядка 105, а bi — порядка 106, числитель и знаменатель дроби могут быть порядка 1011. Когда мы сравниваем дроби  и
и  , мы сравниваем произведения ad и bc, которые по нашим оценкам могут быть порядка 1022. Это, к сожалению, приводит к переполнению встроенных целочисленных типов во многих языках. Чтобы разобраться с этой проблемой, вычтем из всех дробей единицу (очевидно, на порядок сортировки это не повлияет), и теперь отношения для прибавлений выглядят как
, мы сравниваем произведения ad и bc, которые по нашим оценкам могут быть порядка 1022. Это, к сожалению, приводит к переполнению встроенных целочисленных типов во многих языках. Чтобы разобраться с этой проблемой, вычтем из всех дробей единицу (очевидно, на порядок сортировки это не повлияет), и теперь отношения для прибавлений выглядят как 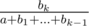 . Теперь, числитель стал всего лишь порядка 106, произведения будут порядка 1017, что уже помещается в стандартный 64-битный тип в любом языке.
. Теперь, числитель стал всего лишь порядка 106, произведения будут порядка 1017, что уже помещается в стандартный 64-битный тип в любом языке.
Challenge: пускай нам надо сравнить две дроби  и
и  , где числа a, b, c, d могут быть порядка 1018. Каким способом вы бы это сделали? Сможете ли вы придумать простое решение, которое не использует длинную арифметику, вещественные числа или волшебные целочисленные типы, такие как
, где числа a, b, c, d могут быть порядка 1018. Каким способом вы бы это сделали? Сможете ли вы придумать простое решение, которое не использует длинную арифметику, вещественные числа или волшебные целочисленные типы, такие как __int128 и им подобные (однако, возможно, совершает неконстантное число операций)?
Идея: Endagorion
Подготовка: Endagorion
Нам нужно найти в неориентированном графе две вершины, такие что их можно соединить тремя вершинно и реберно непересекающимися путями. Это легко решалось бы потоком, если бы не большие ограничения.
Во-первых, заметим, что все пути между двумя выбранными вершинами должны проходить внутри одной двусвязной компоненты графа. Действительно, любой простой цикл должен целиком лежать внутри одной двусвязной компоненты, а набор из трех путей можно представить как объединение двух пересекающихся циклов. Поэтому, сперва выделим все двусвязные компоненты графа и попытаемся решить задачу независимо в каждой из них. Двусвязные компонентны можно найти за линейное время; хороший алгоритм, который это делает, можно найти в статье по ссылке выше.
Теперь, у нас есть двусвязная компонента и та же самая задача. Во-первых, найдем любой цикл в этой компоненте обычным DFS'ом; единственный случай, когда цикл не найдется, — это когда компонента состоит из одного ребра, но это неинтересный случай. Теперь, предположим, что ни из какой вершины цикла не исходит ребра, которое бы не лежало в цикле; в этом случае цикл не связан ни с какой другой вершиной компоненты, поэтому компонента сама по себе является этим циклом; очевидно, что в этом случае решения также нет.
В противном случае, возьмем вершину v, из которой исходит ребро e, не лежащее в выбранном цикле (обозначим цикл за c). Если мы сможем найти такой путь p, который начинался бы с ребра e и заканчивался в какой-то вершине из цикла u (отличной от v), мы сможем выделить три непересекающихся пути между u и v: один из них — это p, а два других — половинки исходного цикла. Чтобы найти путь p, запустим DFS, который начинается с ребра e и заканчивается, как только мы приходим в вершину цикла c, отличную от v, а потом восстанавливает все пути для ответа.
Что же делать, если такого пути p не найдется? Обозначим за C компоненту, которую обошел этот DFS. У него не получилось найти пути между вершинами из множества C\ {v} и множества c\ {v}, поэтому любой путь между этими двумя множествами должен проходить через v. Но тогда оказывается, что если удалить v, компонента C\ {v} оказывается отделена от вершин из множества c\ {v}, что противоречит тому, что исходная компонента была двусвязной. Отсюда следует, что тот DFS, который мы запускали из e, всегда найдет подходящий путь p и получит ответ, если наша двусвязная компонента — не цикл и не отдельное ребро.
В итоге мы пришли к тому, что ответа нет в единственном случае, когда все двусвязные компоненты — либо отдельные ребра, либо циклы; другими словами, когда граф является несвязным набором кактусов. В противном случае, за пару запусков DFS'ов мы сможем найти три непересекающихся пути. В итоге получилось решение за время O(n + m); для упрощения можно было бы где-нибудь накрутить парочку логарифмов.
Challenge: сколько существует графов G, таких что в G можно выбрать две вершины, соединенные тремя непересекающимися путями? (Подсказка: мы знаем, что достаточно посчитать количество несвязных объединений кактусов.) Можете ли вы придумать какое-нибудь полиномиальное по времени решение? Решение за время O(n3)? Возможно, еще быстрее?










Is it possible to do Div 2 B using dynamic programming? I tried to implement this however kept encountering errors, which partially might be because I am getting stuck in some sort of infinite loop of say going from 1 -> 2 -> 1 over and over. However even after I thought I fixed that I still had problems. The two approaches described here in the editorial are obviously better now I see, but I am wondering if anybody successfully implemented a dynamic programming solution, as I would like to understand if this is possible, and if not why this is so? Thanks!
I had a terrible issue with the order of the operations, so I reach the dp[n] with an incorrect timing (amount of steps) then all the calculations from there where straight to hell, my implementation was basically dfs.
Hello =)
I tried DP at first but it gave me wrong answer because I didn't handle the cases like "9999 10000" which the answer is 5000.
But I tried the backwards solution (recently) and got AC:10125859
Dp solution:
codeforces.com/contest/520/submission/10109529
I don't know about a DP solution but a fairly simple recurrence gives the right answer.
I think this is O(log(n)) but still working on Endagorion's challenge to generalizing it for subtract a and multiply b type of operations. Any further hints Endagorion ?
Well, basically the editorial contains everything you need. The case when a and b are coprime seems somewhat easier to handle. =)
For Div-1 C / Div-2 E, I first learned the O(n) modulo inverse computation from rng_58's solution in the TCO10 finals: http://community.topcoder.com/stat?c=problem_solution&rm=306085&rd=14287&pm=11061&cr=22692969
Here's the implementation :)
Can problem B Div-1 be solved if the number was constructed from the right to the left?
520B - Two Buttons I know that turning m into n is easier than the opposite, but why is this code wrong? Can you give me any easy counterexample?
5 11
Correct solution:
5->4->3->6->12->11 — 5 steps
Your solution:
5->10->9->8->7->6->12->11 — 8 steps
You are wrongly assuming that if n is 2 times or more smaller than m it is worth everytime to multiplky n by 2. Look at the example. Even though you quickly got to 10 which is so close to 11 you then have to subtract one so many times that it becomes inefficient. Intuitevely it is better and faster to get to 3 first, because difference between 5 and 3 is small, as they are are small numbers and then multiplyinyg that 3 by two will quickly get you to 12 — closest even number to 11.
Yeah, you are right! Do you think it is possible to solve this problem converting n into m?
Possible but tough!
missing the challenge part like the previous editorials of Endagorion
Ah, yes, I knew I forgot something. I'll put them up shortly, stay tuned.
Can anynone explain the fast solution of the div 2 b problem with an example ??
Its quite simple . First understand if m<n then ans is n-m
else
make m less than or equal to n by dividing it by 2 , increase the count by one and if at any moment it becomes odd increase the count by 1 and increase m by 1 . e.g
4 17
1. 17->18
2. 18->9
3. 9->10
4. 10->5
5. 5->6
6. 6->3
then 3 is smaller than 4 so ans is 6+(4-3) = 7
nyways take a look at my solution 10105430 . Its quite easy to understand .
how can we approch this problem by using graph
can anybody find mistake in my solution of 521C - Pluses everywhere? it doesn't come through the 10 test :/ and i'm out of guesses now
Here is my code http://pastebin.com/aH1u9vmv (updated, now commented) sorry for my horrible english
Same here, hope somebody would help.
Never mind, it was a simple bug in my nCr function :S
Бонус к D : разложить и
и  в цепные дроби и сравнить цепные дроби (в каждой цепной дроби числа не будут превосходить 1018). Цепные дроби сравниваются поиском первого различия (для удобства можно дописать в конец каждой дроби 1018 + 1 (или любое другое большое число, влезающее в long long)). Асимптотика
в цепные дроби и сравнить цепные дроби (в каждой цепной дроби числа не будут превосходить 1018). Цепные дроби сравниваются поиском первого различия (для удобства можно дописать в конец каждой дроби 1018 + 1 (или любое другое большое число, влезающее в long long)). Асимптотика 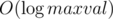 , где maxval — ограничение на числа.
, где maxval — ограничение на числа.
Да, все так.
Is it still possible to solve problem 1B/2D, if we allow same number appearing multiple times?
Вроде есть на емаксе
Возможно я где-то ошибся, но вроде бонус к первой задаче делается за логарифм от n(если считать размер алфавита константой и ответ выводить по какому-нибудь модулю):
Сначала избавимся от больших и маленьких букв, для этого умножим в конце ответ на 2^n. Потом можно написать на искомое выражение формулу включений-исключений(там придётся посчитать все сочетания из k элементов, где k — размер алфавита, что делается за O(k^2) или за O(k), если модуль хороший, и умножать их на числа в степени n). Таким образом асимптотика будет O(k^2 + klogn). Это, если я правильно понимаю, что challange и задача по ссылке по сути эквивалентны, рассказывалось в ЗКШ(там же и все формулы, которые я, для краткости, опустил): http://opentrains.mipt.ru/zksh/files/zksh2015/lectures/zksh_upd.pdf ( последние 2 страницы)
Div1D challenge:
This should be correct up to den=0 and maybe some negative values, but it's not a code I will use, so details are left to the reader, it's just a main idea :P.
Best problem E ever in Codeforces. No any complex ideas but very very very insightful
Div1C challenge:
Consider i-th position:
amount of expressions consisting ai with multiplier 100: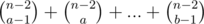 ,
,
with 101: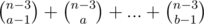 ,
,
...
with 10n - i - 1: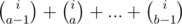 ,
,
with 10n - i: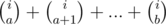 .
.
One should compute this numbers and it's prefix sums only ones.
The main task is calculating for all n ≤ 105 and few number of k.
for all n ≤ 105 and few number of k.
This can be done in linear time for each k:
Yup, that's it.
CUBES: What is so particular with test case 19 ?? For all previous tests my code (java) runs below 500 ms . And I get timed out for test 19...
Maybe it is something like anti-java-hashmap test.
My current code doesn't use HashMap. I do some sorting and binarySearch at the begining to initialise my data structure. After,I use a PriorityQueue, but with Integer objects (the objects beeing the value of the cube). It's annoying me...
I used two priority queues. I replaced by one TreeSet. That changed performance on test19....
Thanks you, I get this error too and after change from PriorityQueue to TreeSet the performance is better and I get AC. It's seem the operator add in TreeSet better PriorityQueue in this case.
I dont understand how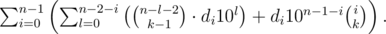 becomes
becomes 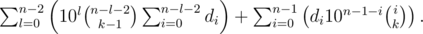
Please can anyone explain?
The first part of the sum: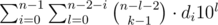 =
= 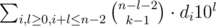 =
= 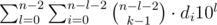 =
= 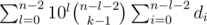 . The second part stay the same.
. The second part stay the same.
Is that any more transparent?
Thanks Endagorion. I got it.
:)
Excuse me, someone can explain Div D example test case, I don't understand this line: "assign the i-th skill to b;"
Can anyone please explain the challenge of Div 2 C/ Div 1 A(DNA Alignment).
Isn't the challenge for A just the number of surjections {1, 2, ..., n} → {'a', ...'z'}?
Note that n, m, k are all independent parameters.
520A Challenge: Would (26 * n) be considered a linear time?
What about a dp with index and count of distinct lower-case characters that showed up till now? Time: 26 * n. Memory: if converted to a loop, would be something like 26 or 2 * 26.
Edit: Of course, there's some memoization and modding.
can any one please tell me the generalize solution of Div2 B problem , when instead of 2 and 1 , a and b are given ?
wow, I only know better algorithm solving B problems after reading this post
Hi, I'm having trouble understanding why my code fails on test 4 of D2D. Here is my solution which swaps 4 and 6 in the 4th test for some odd reason. I'd appreciate the help! Thanks.
Submission Link
EDIT: Nvm I found the issue, I didn't exclude values after updating.
520B — Two Buttons I found an elegant solution after looking through the confusing editorial. The algorithm with complexity O(log m + Δ), where Δ is a difference between m and n.
My code here
Feel free to leave any feedback.