Given a non self-intersect polygon and a line. How can I calculate the total length of parts of line which are inside the polygon? I need an O(NlogN) or faster algorithm, where N is the number of vertices of polygon.
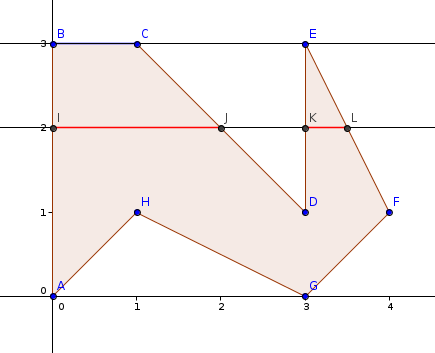
For example, below is the polygon ABCDEFGH.
With line y = 0, no parts inside the polygon.
With line y = 2, the parts inside the polygon are IJ and KL, and the total length is 2.5.
With line y = 3, the part inside the polygon is BC, which has length 1,
I'm looking for your answers. Thanks for your help.











I'm also !
Do you know how to cut a polygon with a line? It is similar. The main idea is to keep track of where you are respectively to the line while going through vertices of the polygon.
If you do this properly, you get 2k points of intersection between the line and the polygon. Then you can easily get the total length.
I think that we can sort the intersections of the given line with the polygon's edges by their X-coordinate (tie by Y-coordinate). Then the result should be the total distance between every pair of points i and (i+1) (with i%2=1)
Can you explain more about your solution? I'm afraid it doesn't work in case y=0 or y=3 above.
I think it still work. You should not eliminate intersections which have the same X and Y coordinates then it would work.
How about y = 1 ?
The intersections are (0, 1), H, D, and F. All segments are inside the polygon.
Your answer is (0, 1) -> H + D -> F. It's wrong.
It should be (0,1)->H+H->D+D->F? :-?
how about y = 2 ?
It's kinda obvious with y=2 you know. And I am really frustrated since I am just sharing my thoughts and all I got is down votes? So like only people with top ranks should have the right to vote hah?
the right to speak sorry ...
You can't consider the segments of the polygon separatedly. Counter example:
Counterexample
On the left, you need to remove the intersection. On the right, you must not. Both have 2 segments touching the line.
We could however resolve this issue by looking at the other segment sharing the vertex/point/endpoint (when the line intersects the polygon at an endpoint). If both segments have their other endpoint on the same side of the line, then the intersection should be removed, otherwise it should not.
(Your main point is still valid though, i.e., we can't consider segments individually. But TiChuot97's solution is quite appealing in its logical simplicity, so I think we should try to save it. =D )
You're right. Actually my previous comment "keep track of where you are respectively to the line while going through vertices of the polygon" means the same as what you said (though probably I made it sounds scarier).
Yeah I got it now, but I think that I've read an article somewhere which approached the problem similarly to what I did. So thanks for the counter example.
Let's divide the polygon trapeze height 1 (h = 1)
For trapeze as AQH (point Q(0;1) ) or GHF we consider that the base is 0 (points A or G)
Let's count areas of all trapeze (S (trapeze) = h * (a + b) / 2, h = 1 => S (trapeze) = (a + b) / 2)
S(AQH) = QH / 2, S(GHF) = FH / 2 = (HD + DF) / 2 S(QIJD) = (IJ + QD) / 2 = (IJ + QH + HD) / 2 S(DKLF) = (KL + DF) / 2 S(IBCJ) = (BC + IJ) / 2, S(KEL) = KL / 2
if we sum all areas, we'll have: 1)area of polygon 2)QH + HD + DF + IJ + KL + BC/2 BC — horizontal side
So we should count half-sum of all horizontal sides of the polygon, because we consider them once
So ans = Area of polygon + Half-sum of all horizontal sides of the polygon
I'm looking for a site where I can submit my solution. Would you help providing the link?
I ask this in order to solve a problem with Vietnamese statement. Unfortunately, I don't know any other problems using this one.
Edit: sorry, misread the statement.
Poor you =))
Just to explain why flashmt is explaining solution of non-related problem: I_love_tigersugar used the example figure of this famous problem in Vietnamese OJ, so flashmt probably did not read the statement again and write solution.
The problem statement of this problem goes like this: