Hello, this is a post for beginners. Recently I came across a blog of someone asking a very basic simple explanation. I will try my best to explain DFS in as a simple a way as possible. Note, If you know DFS, don't read any further.

DFS (Depth First Search) is an algorithm used to traverse graph or tree. We first select the root node of a tree, or any random node(in case of graph) and explore as far as possible in a branch and then come back to a fixed point. DFS is generally used for connectivity questions. It has a time complexity of O(N+E) Where N is the total number of nodes and E is the total number of edges.

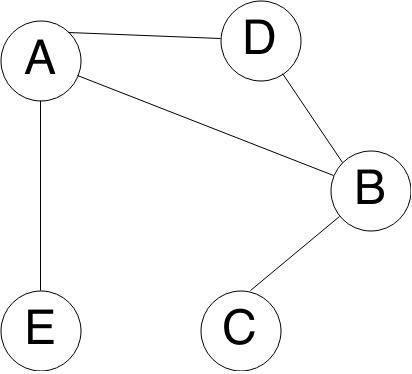
Let's take this graph. Here A is connected to E,B,D ; B is connected with A,D,C ; C is connected with B ; D is connected with A,B and E is connected with A ; F is not connected.

We represent this graph using an Adjacency List. Here is the code (in Python)

graph={ 'A':['E','B','D'],
        'B':['A','D','C'],
        'C':['B'],
        'D':['A','B'],
        'E':['A']}

Once we have the list, we perform DFS. Basically, we pick a node. Then we keep track if we have visited the nodes directly and indirectly connected to it. Since we are traversing downwards, we use a stack and we'll use it's last in first out(LIFO) feature. We also keep a list of all the nodes we have visited since we have to visit each node only once. So we will add an node to the stack only if that node has not been visited. On visiting a particular node we remove it from the stack. Finally, we'll end up visiting all the nodes and then the stack will be empty. That will serve as the terminating condition.

Here are the steps to follow while performing DFS.

• Select a node. Since we have selected the node, add it to the visited list.
• Look at all the adjacent nodes. Add those nodes which have not been visited to the stack.
• Then pop the top node and Follow the first two steps.

Now, let us pick any node (say A) and perform DFS.

1. We have selected the node A. We now add A to the list of nodes we have visited(which is empty initially). The nodes directly connected to A are E,B,D. So since we havent visited those nodes, we add them to the stack s. Now s=[E,B,D] and visited=[A]
2. We pop s, and we get D. Now D is connected directly with A,B. Since we have visited A, we dont add it. So now s=[E,B] and visited=[A,D].
3. We pop s, and we get B. Now B is connected directly to A,D,C. Since we have visited A,D we dont add it. However as we have not visited C, we add it to stack s. So now s=[E,C] and visited=[A,D,B]
4. We pop s, we get C. Since we have visited all nodes connected to C, we dont push anything to the stack s. So now s=[E] and visited=[A,D,B,C]
5. We pop s, we get E. Since we have visited all nodes connected to E, we dont push anything to the stack s. So now s=[] and visited=[A,D,B,C,E]

Now the stack is empty, and the DFS has been completed. The answer lies in the order we visited in the visited list.

Sample iterative implementation.

graph={ 'A':['E','B','D'],
        'B':['A','D','C'],
        'C':['B'],
        'D':['A','B'],
        'E':['A']}

def dfs(graph,s):
    stack=[]
    visited=[]
    stack=[s]
    while stack:
        node=stack.pop()
        if node not in visited:
            visited.append(node)
            stack=stack+graph[node]
    return visited

Hope this helps you.

Thanks for your attention :) :)