Набор задач в онлайн-трансляции незначительно отличается от набора задач на основном раунде, задачи следуют в порядке, в котором они фигурируют в основном раунде.
524A - Возможно, вы знаете этих людей?
В задаче требовалось реализовать ровно то, что описано в условии. Фиксируем человека x, проходимся по всем остальным людям y, не дружащим с x, и считаем количество общих друзей x и y.
Тонкий момент №1: несмотря на то, пар друзей во вводе не более 100, самих людей может быть до 200, и можно ошибиться в выставлении размеров массивов.
Тонкий момент №2: нужно аккуратно сравнивать вещественные числа. Если написать нечто вроде common / degree >= k / 100.0, то в силу специфики вычислений с вещественными числами, результат такой проверки может быть недетерминирован (если в какую-то из частей внесётся незначительная погрешность). Поэтому, надо либо сравнивать с точностью до некоторого eps, либо выполнять проверку в целых числах: common * 100 >= degree * k.
524B - Фото на память - 2 (round version)
Переберём высоту итоговой фотографии. При фиксированной высоте нам требуется минимизировать суммарную ширину всех прямоугольников. Таким образом, для каждого прямоугольника нужно выбрать такое из двух его положений, которое, во-первых, подходит по высоте, а во-вторых, имеет меньшую возможную ширину.
529B - Фото на память - 2 (online mirror version)
В версии для онлайн-трансляции условие было незначительно изменено — разрешается, чтобы не более n / 2 людей лежали на фотографии. Это слегка усложняет решение. Введём терминологию: людей, у которых w ≤ h, будем называть высокими, а остальных людей — широкими. Зафиксируем итоговую высоту фотографии H. Далее, следует небольшой разбор случаев.
- Если высокий человек влезает под высоту H, то мы его оставляем именно в таком состоянии.
- Если высокий человек не влезает под высоту H, то мы обязаны его положить, увеличиваем счётчик таких людей на 1.
- Если широкий человек влезает под высоту H, но не влезает, будучи положенным, то ставим его.
- Если широкий человек влезает под высоту H обоими способами, то сначала ставим его, а в отдельный массив выписываем величину, на которую уменьшится ответ, если этого человека всё-таки положить: w - h.
- Если же кто-то не влезает ни одним из двух способов, то подобное значение H недопустимо.
Теперь у нас есть какое-то количество людей, которые обязательно должны лечь (из второго пункта), причём, если их слишком много, а именно, больше, чем n / 2, то подобное значение H недопустимо.
За вычетом людей из второго пункта у нас осталось некоторое количество вакантных лежачих мест — распределяем их по людям из четвёртого пункта в порядке уменьшения величины (w — h). Считаем площадь фотографии, выбираем минимум по всем H.
524C - Искусство обращения с бакноматом
Предполагаемое решение имеет сложность 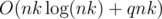 или
или 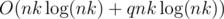 . Для каждой возможной суммы денег x = t·ai (1 ≤ t ≤ k) выпишем пару (x, t) в массив, здесь t — количество купюр, которым такую сумму можно достичь. Отсортируем этот массив. Тогда чтобы ответить на один запрос, переберём первое слагаемое в сумме, а второе либо найдём бинарным поиском, либо воспользуемся методом двух указателей, чтобы найти парное слагаемое за амортизированное время O(1). Проверим, что получилось не более k купюр в сумме, улучшим ответ, если надо.
. Для каждой возможной суммы денег x = t·ai (1 ≤ t ≤ k) выпишем пару (x, t) в массив, здесь t — количество купюр, которым такую сумму можно достичь. Отсортируем этот массив. Тогда чтобы ответить на один запрос, переберём первое слагаемое в сумме, а второе либо найдём бинарным поиском, либо воспользуемся методом двух указателей, чтобы найти парное слагаемое за амортизированное время O(1). Проверим, что получилось не более k купюр в сумме, улучшим ответ, если надо.
524D - Социальная сеть
Будем жадно действовать следующим образом. Идём по запросам в порядке поступления. Каждый очередной запрос пытаемся сопоставить новому человеку. Разумеется, это не всегда возможно сделать — если у нас уже есть M активных людей на сайте, то мы обязаны сопоставить очередной запрос кому-то из них. Возникает вопрос — кому именно?
Можно показать, что выгоднее всего сопоставить этот запрос самому недавнему из активных людей. Действительно, подобное “критическое” (по количеству людей) состояние можно задать вектором из M чисел — временами с момента последнего запроса каждого из людей в убывающем порядке. Тогда если сейчас состояние — (a1, a2, ..., aM), то мы можем перейти в одно из M новых состояний (a1, a2, ..., aM - 1, 0), (a1, a2, ..., aM - 2, aM, 0), ... , (a2, a3, ..., aM, 0), в зависимости от того, к кому мы подцепим очередной запрос. Видно, что самый первый вектор покомпонентно больше, чем любой из оставшихся, а это значит, что он выгоднее всех остальных (т. к. чем больше число на определённой позиции в векторе, тем скорее может исчезнуть этот человек, и тем больше у нас остаётся свободы для последующих действий).
Значит, нам требуется моделировать процесс, поддерживая в некоторой структуре данных множество активных людей с временами их активности. В качестве подобной структуры можно воспользоваться любой структурой, реализующей интерфейс очереди с приоритетом (priority_queue, set, дерево отрезков или что-либо ещё). Итоговая сложность решения —  .
.
524E - Ладьи и прямоугольники
Поймём, что означает тот факт, что какая-то клетка прямоугольника не побита ладьёй. Это значит, что существует строка прямоугольника, не содержащая ладью, и существует столбец прямоугольника, не содержащий ладью. Не очень ясно, как проверять это утверждение, поэтому проверим обратное к нему — мы только что показали, что прямоугольник является покрытым, если либо в каждой строке стоит ладья, либо в каждом столбце стоит ладья.
Эти утверждения можно проверять по отдельности. Как проверить для набора прямоугольников, что в каждой строке находится отмеченная точка? Это можно сделать за один проход вертикальной сканирующей прямой. Пусть мы идём слева направо и прошли через правую границу прямоугольника, расположенного в строках с a-й по b-ю, левая граница которого находится в столбце x. Тогда если обозначить за last[i] позицию последней ладьи, встреченной в строке номер i, то критерий для прямоугольника выглядит следующим образом: 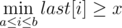 . Это значит, что для хранения величины last можно воспользоваться деревом отрезков. Аналогично проверяем для столбцов. Выходит решение, отвечающее на все запросы off-line за время O((q + k)log(n + m)).
. Это значит, что для хранения величины last можно воспользоваться деревом отрезков. Аналогично проверяем для столбцов. Выходит решение, отвечающее на все запросы off-line за время O((q + k)log(n + m)).
524F - И снова правильная скобочная последовательность
Общая идея заключается в том, что скобочные последовательности можно рассматривать как последовательности балансов префиксов, т. е. как последовательности чисел (ai), где ai + 1 = ai ± 1.
Посчитаем количество открывающихся скобок A и закрывающихся скобок B в исходной строке. Заметим, что если A > = B, то строку всегда можно исправить, дописав A - B закрывающихся скобок в конец, и циклически сдвинув строку в точку минимума баланса, а если A ≤ B, то строку аналогично можно исправить, дописав B - A открывающихся скобок в начало. Очевидно, что меньшим количеством скобок не обойтись. Таким образом, мы уже знаем величину ответа, теперь нужно понять, как он устроен.
Будем считать, что мы сначала производим циклический сдвиг, а потом только добавляем скобки. Пусть, для определённости, мы дописываем x закрывающихся скобок. Сформулируем два несложных утверждения:
- Если путём дописывания в определённые x мест закрывающейся скобки, строку можно сделать правильной скобочной последовательностью, то её также можно сделать правильной дописывая x закрывающихся скобок просто в конец.
- Из всех строк, которые можно получить дописыванием в произвольные x мест закрывающейся скобки, минимальной является та, в которой скобки дописываются в конец.
Каждое из этих утверждений несложно проверить, а в совокупности они нам дают тот факт, что в оптимальном ответе мы дописываем закрывающиеся скобки в конец строки. Значит, нам надо рассмотреть множество таких циклических сдвигов строки, что они превращаются в правильную скобочную последовательность при приписывании в конец x = A - B закрывающихся скобок (т. е. просто не имеют нигде отрицательного баланса), и выбрать из них лексикографически минимальный. Сравнение циклических сдвигов строки можно проводить либо при помощи суффиксного массива, либо же, так как нам требуется только найти минимальный сдвиг из определённого множества, можно сравнивать сдвиги между собой при помощи бинарного поиска и хеширования.
Аналогично делается случай, когда A ≤ B, с единственным отличием, что открывающиеся скобки дописываются в начало.
Таким образом, выходит решение за сложность  .
.











Thanks for editorial, F is good)
В задаче С можно получить O(q * n * k) без сортировок за счет маленьких ограничений — заведем массив char на 2*10^8, и для каждой позиции посчитаем, какое минимальное число банкнот одного номинала нужно, чтобы выдать соответствующую сумму. Тогда для ответа на запрос нужно перебрать n*k вариантов первого слагаемого, а для каждого такого варианта ответ можно будет доставать из нашего массива за О(1).
В задаче D легко получается линейная сложность. Заведём массив размера N, в котором мы будем хранить времена предполагаемого выхода пользователей с сайта. На этом массиве мы поддерживаем указатели на текущее множество активных людей, изначально они равны нулю. Тогда при очередном запросе нам достаточно проверить, М людей сейчас активны или нет. Если М, то мы обновляем время выхода человека с максимальным id, иначе добавляем нового пользователя (двигаем правый итератор на 1), таким образом, видно, что времена выхода у нас отсортированы автоматически. Для удаления достаточно двигать левый итератор вправо, получаем линейную сложность.
Или можно просто завести deque вместо priority_queue, потому что все удаляется с начала и иногда заменяется последний элемент
Да, что-то я переборщил в этом месте. Безусловно, вы правы.
В задаче E, видимо, не x, а y в условии проверки.
Да, поправил.
it's not necessary to use data structures in problem D , it can be solved in O(n) here is my submission 10386806
During the contest, I had all of that for F (A in mirror) except
I couldn't prove that it was always possible to make the string work using the lower bound of |A - B| brackets (indeed I thought this wasn't true, didn't even submit as a guess). How can you prove this?
Lets say the length of the string is N for convenience. In the string, let '(' be +1 and ')' be -1. For a balanced string (equal number of '(' and ')' ), the total sum of the string will be 0.
In order to make any balanced string a valid sequence, first write out the prefix sums of the string (with +1 and -1). If the indexes are 0-indexed, then the prefix sum at i: PSi = S0 + S1 + ... + Si. We want to shift the string such that PS0, ..., PSN - 1 ≥ 0
Next, find the index at which PS is minimum (any index will do if there is a tie), call this index x ( PSx = min(PS0, ..., PSN - 1) ). Let's call S[0...x] A, and S[x + 1...N - 1] B.
Now, if PSx ≥ 0, the sequence is already valid.
If not, then we shift B to the beginning of the string. So if before S = A + B, now S' = B + A. Note that the sum of B is - PSx, so in S' = B + A the minimum prefix sum in A will be - PSx + PSx = 0. Additionally, we know the minimum in B can't be less than 0, or else there would have been an element less than PSx in S = A + B. Hence, S' = B + A will "fix" the string, as all prefix sums will now be greater than or equal to zero.
А в задаче Е отсекались решения за лог квадрат на запрос?
Ну конечно, Zlobober лично все решения смотрел, и отсекал
А разве если мы проверяем покрытие поля отдельно для столбцов и отдельно для строк, итоговая оценка сложности будет не O((q + k) * (log(n) + log(m))), т.е. O((q + k)*log(n * m)) Извините, не очень понимаю, почему O((q + k) * log(n + m))?
O(log(n^2)) = O(log(n))
Что все равно не отвечает на вопрос, почему log(n+m).
Или так пишут исходя из принципа, что max(n, m) <= n + m?
именно, но + короче
Да, моя мотивация была именно такой. Если писать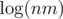 , как вы предлагаете, то это запутывает, т. к. вознкиает ощущение, что логарифм берётся от площади поля. А если писать
, как вы предлагаете, то это запутывает, т. к. вознкиает ощущение, что логарифм берётся от площади поля. А если писать 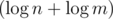 , то выходит длинно.
, то выходит длинно.
There exists O(n) solution of F.
Sequence of brackets can be considered as function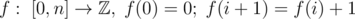 , if S[i] is opening, and - 1 in other case. Sequence of brackets is correct if and only if f ≥ 0 and f(n) = 0. As in
, if S[i] is opening, and - 1 in other case. Sequence of brackets is correct if and only if f ≥ 0 and f(n) = 0. As in  solution, note that
solution, note that
additional brackets can be defined from f(n)
additional brackets in optimal solution go continuously (as single segment)
Lets precompute f, minleft[i] = min {f(j)|j < i}, minright[i] = min {f(j)|j > i}, increasing[i] = (length of maximum increasing sequence with beginning at f(i)).
New observation: let's consider f(n) < 0 and add - f(n) opening brackets before position i. In this case f(j), j < i will remain still, and f(j), j > i will increase by - f(n). Having minleft and minright, it is easy (O(1)) to check whether we will get correct sequence (shifting string if necessary).
Using previous observation and precomputed array increasing, we determine all positions where we can get correct sequence and choose only ones with maximum increasing[i].
After that, we use idea of two pointers (first and second) to find ultimate best position. First and second point to beginning of comparing subsequences. Obviously, these pointers must be ones of previous computation. This method gives linear time because we can keep comparing sequences not intersected: if on some step sequences are going to become intersected, we move one of pointers in the position after it's sequence and start comparison anew.
For example first = 0, second = 3
abcabcd
S[first + i] = S[second + i] for i = {0, 1, 2}
we move second to 6 and start comparison anew, comparing
S[first + i] with S[second + i] (first = 0, second = 6, i = 0, 1, ...)
instead of
S[first + i] with S[second + i] (first = 0, second = 3, i = 3, 4, ...)
because we already found out that S[0, 1, 2] = S[3, 4, 5].
I added some comments in hope that my code will help to figure out solution. http://mirror.codeforces.com/contest/524/submission/10398060
Вопрос снят
Where that comes from in F? It's clearly O(n). In CF when
comes from in F? It's clearly O(n). In CF when  is expected then constraints are at most 3·105 or sth, so I was afraid that
is expected then constraints are at most 3·105 or sth, so I was afraid that  can be too slow and coded O(n) solution. Suffix array can be constructed in O(n) and it is well known that we can get minimum values on all intervals of length k for a fixed array (which is necessary to check which shifts are allowed). Check my solution here: 10386965
can be too slow and coded O(n) solution. Suffix array can be constructed in O(n) and it is well known that we can get minimum values on all intervals of length k for a fixed array (which is necessary to check which shifts are allowed). Check my solution here: 10386965
Well, as far as I can tell usually it's not expected from participants to build suffix array in O(n) (Actually it's just dew times faster than NlogN version).
As for constraints, note 5s TL.
BTW, our NlogN solution takes just 0.5s, while your O(N) works in 1.8 :)
10382149
Problem 524D (Social Network) can be solved in O(N), not in O(N ln N), if a circular buffer is used to keep non-expired users.
All operations happen with ends of user queue. New users are pushed to one end, last user's time is changed for a user from same end. Expired users are removed from another end. Pushing and updating time is O(1) per one operation, removing expired users is O(N) for all of them, because eventually we remove less then N users.
Check my solution here: 10480700
Hi
Can someone explain the solution of the problem E — Rooks and Rectangles in detail? Help is appreciated.
I love you.
I love you, too.
I also love you.
Problem F can be solved in O(N) time using the skew algorithm.
My brute force solution making roughly 5e8 operations in total passed for problem C The Art of Dealing with ATM. The solution is as follows:
Let us solve first query with value $$$x_1$$$. Pick a denomination and choose the number of times (
<=k) you'll use it. This will be $$$5000\times k$$$ combinations. For each choice, you'll be left with some remainder $$$r = x_1 - c * d_i$$$, where you had chose the $$$d_i$$$ denomination $$$c$$$ times.If $$$r=0$$$ we are done. Else, since the ATM only allows two different denominations, there must exist some $$$c_2 \le k - c$$$ such that $$$r$$$ is divisible by $$$c_2$$$ and $$$d_j = r / c_2$$$ is another denomination that exists in the set of all denominations. You can loop for all such $$$c_2$$$ and check for existence of $$$d_j$$$ in $$$\log n$$$.
In the end, complexity for one query is $$$5000\times k \times k \times \log 5000$$$. We have twenty such queries. So, expected complexity is around $$$4.91e8$$$ operations. It is still surprising to me that this passed by a really decent margin (293ms out of 2000ms allotted).
Submission link
Could you tell me how to find lexicographical minimum by using hashing and binary search in problem F? Thank you very much.