Добрый день! Недавно я столкнулся с интересной математической задачей: "Докажите, что если в куб можно поместить три шара радиуса 1, то можно поместить и четыре шара радиуса 1".

Чтобы решить задачу, ее нужно немного переформулировать. Рассмотрим внутренний куб, все стороны которого отстоят от внешнего на 1. В этом внутреннем кубе лежат центры шаров, притом расстояние между любыми двумя не меньше 2. Введем функцию f(n) — минимальный размер куба, в который можно поместить n точек так, что расстояние между любыми двумя не меньше 2. По сути, в задаче требуется доказать, что f(3) = f(4) (и на самом деле они обе равны 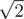, как показывает несложный анализ).

Равенство 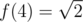достигается на очень простой конфигурации — надо поместить четыре точки в вершины куба через одну. И тут мне стало интересно — а как посчитать f(5), и как выглядит оптимальная конфигурация в таком случае?

Математические рассуждения, прокатывавшие для 3 и 4, тут уже, к сожалению, не работают. Я решил воспользоваться компьютером, и реализовал алгоритм, работающий на следующих рассуждениях: Во первых, зафиксируем размер куба как 1, и будем решать такую задачу: для каждого расположения точек в кубе мы запишем минимальное расстояние между точками, и это минимальное расстояние должно быть максимальным. Ясно, что .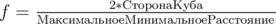

Заметим, что если взять любое расположение точек в кубе, и сдвинуть каждую точку не более, чем на x, то любое расстояние изменится не более, чем на 2x. Разобьем наш куб на 3 * 3 * 3 маленьких кубиков. Будем считать, что все точки самой удачной конфигурации лежат в этих центрах этих маленьких кубов — и переберем всевозможные комбинации. После этого можно считать, что точки из самой удачной конфигурации лежат на расстоянии не более 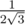(это половина диагонали куба со стороной ) от полученных точек, поэтому вокруг каждой мы можем нарисовать куб, и считать, что точки из самой удачной конфигурации лежат в этом кубе. На следующей итерации мы делим получившиеся кубики на меньшие (3 * 3 * 3), и начинаем перебирать (считаем, что первая точка теперь находится в первом кубе, вторая во втором, и т.д.). В конце каждой итерации мы получаем оптимальную конфигурацию с определенной точностью, и вновь повторяем процесс. Минусы такого подхода очевидны: на любой итерации перебирается 27⁵ случаев, что приблизительно равно 10⁷. Тем не менее, где-то за 20 минут компьютер с хорошей точностью посчитал f(5) как 1.7889, что практически равно 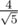. Соответственно, самая выгодная расстановка 5 точек в кубе: (0, 0, 0), (1, 0.5, 0), (0.5, 0, 1), (0, 1, 0.5), (1, 1, 1) (в относительных координатах). Если f(6) еще можно будет посчитать за адекватное время, то нахождение f(7) выглядит уже достаточно сложной задачей.

Таким образом, хотел бы послушать еще какие-нибудь полезные идеи по поводу алгоритма:)

P.S Оказалось, что результат для f(6) довольно тривиален — это 2, равенство достигается, когда мы просто суем точки в вершины куба. Отсюда следует, что f(7) = f(8) = 2. В общем, теперь жду каких-то интересных комментариев по поводу того, как посчитать f(9) :)