UPD: I cannot fully understand Xellos' solution but a friend of mine(radoslav11) wrote this code and got AC with it. The bad thing is that neither me nor him can prove the correctness of the algorithm. At least for me this seems not to be right:
if(v != parent[u])
low[u] = min(low[u], low[v]);
Can anybody prove the correctness of the code or give a counter example and if such example exists can you explain in details another algorithm that is correct, please? :)
Hello everybody,
Recently, I started learning about articulation points, bridges, bi-connected components and strongly connected components. I decided to solve some problems from lightoj and I can't solve this one.
In short, you are given an undirected connected graph with N vertices and M edges (N<=10000, M<=20000). Find the minimum edges we need to add so that the graph should not contain a bridge.
Can anybody tell me what the solution is and prove its correctness since I came up with some algorithms that seemed correct to me but after a while I found some counter-examples, please? And can you give me some problems to solve involving those topics because now the seem kinda confusing to me and I think that I need to practice more, please?
Another question that I want to ask is: I know that a bi-connected graph is a graph without articulation points. But is it true that if a graph doesn't contain a bridge, then it is bi-connected and is it true that if a graph is bi-connected, then it contains a bridge and why?
Thanks in advance!











We can compress any 2-connected component into a vertex without changing the problem, which makes the graph a tree, so let's solve the problem on trees.
If the tree has L leaves, you can only un-bridge 2 of them by adding an edge, so the lower bound is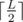 edges.
edges.
On the other hand, you can always pick the edges to add in such a way that all the cycles they induce (in the original tree) pass through one vertex, so there's no bridge left afterwards. Let's focus on the case with L even, where each edge connects a pair of leaves, since adding a leaf and a suitable edge from it if L is odd is trivial.
There's a vertex such that each of its sons' subtrees contains at most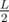 leaves. The proof is similar to the proof of existence of centroid(s): if it's false for some vertex v, then exactly one of its sons violates this property, we can move from v to that son, which doesn't increase the maximum number of leaves of any of its sons; this movement along the tree is therefore monotonous (we never move from v and then to v) and must stop at a suitable vertex.
leaves. The proof is similar to the proof of existence of centroid(s): if it's false for some vertex v, then exactly one of its sons violates this property, we can move from v to that son, which doesn't increase the maximum number of leaves of any of its sons; this movement along the tree is therefore monotonous (we never move from v and then to v) and must stop at a suitable vertex.
If we have this vertex, we can always pair up leaves in its sons' subtrees in such a way that no two leaves in a pair belong to the subtree of the same son. Proof: always take leaves from the subtree/s that have the most of them remaining.
Here is the same problem on CF: Road Problem