Всем привет. Встретил одну интересную задачу по математике, с какой-то олимпиады, но не смог решить. У кого есть идеи?
Имеется n городов и несколько самолетов. Каждый самолет летает только между двумя городами и между любыми двумя городами летает не более одного самолета. Найти минимальное количество самолетов так, чтобы при любой организации авиарейсов из каждого города можно попасть в любой другой не более чем с одной пересадкой.










Подобная задача было на одном контесте (не помню, как она называется). Если я правильно понял, то минимальное число самолётов — n-1. Идея такая: выберем один из городов в качестве хаба. Из всех остальных городов пустим туда авиарейсы. Таким образом, в любой другой город можно попасть из текущего, совершив не более одной пересадки.
не более чем с одной пересадкой
Так и выйдет: путь из каждой вершины до любой другой будет проходить через максимум одну вершину. Картинка для пояснения идеи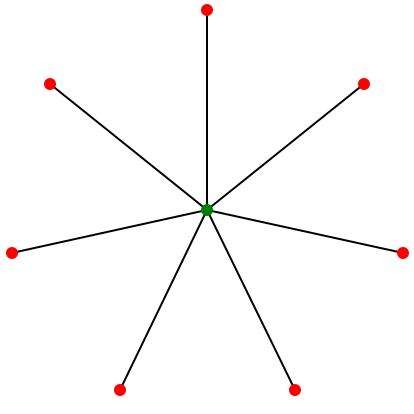
при любой организации авиарейсов
Рассмотрим худший случай: Имеется полный граф с n-1 вершинами, количество ребер будет равно (n-1)*(n-2)/2. Ответ будет (n-1)*(n-2)/2+1 для n>=2.
Точно, большое спасибо!
Доказательство: Из этого следует, что каждый город гарантированно соединен с кем-либо. Пусть m-количество ребер, знаем m>=(n-1)*(n-2)/2+1 Допустим есть два города расстояния между ними,которая больше двух. Посчитаем максимальное возможное количество ребер, соединим все вершины кроме этих двух, то есть (n-2)*(n-3)/2. Первая вершина соединена x-вершинами, вторая y-вершинами. И заметим множество вершин x не пересекается со множеством вершин у, то x+y<=n-2. Максимальное количество возможных ребер будет (n-2)*(n-3)/2+x+y<=(n-2)*(n-3)/2+n-2=(n-1)*(n-2)/2-1<(n-1)*(n-2)/2+1<=m, что невозможно. Значит для (n-1)*(n-2)/2+1 ребер не существует вершин, которые отдалены друг от друга больше чем на 2. Ответ меньше не может быть, т.к может существовать вершина не соединенная ни с кем.