Is there a stupid trick to calculate n-choose-k for a range of n with k always the same, which is faster than forming the full Pascal's triangle? With some fixed k, I need to calculate all n-choose-k modulo 10^9+7 for n up to 100,000 but there's no way I can calculate all the coefficients within 3 seconds.
→ Обратите внимание
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | Benq | 3792 |
| 2 | VivaciousAubergine | 3647 |
| 3 | Kevin114514 | 3603 |
| 4 | jiangly | 3583 |
| 5 | turmax | 3559 |
| 6 | tourist | 3541 |
| 7 | strapple | 3515 |
| 8 | ksun48 | 3461 |
| 9 | dXqwq | 3436 |
| 10 | Otomachi_Una | 3413 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | Qingyu | 157 |
| 2 | adamant | 153 |
| 3 | Um_nik | 147 |
| 4 | Proof_by_QED | 146 |
| 5 | Dominater069 | 145 |
| 6 | errorgorn | 141 |
| 7 | cry | 139 |
| 8 | YuukiS | 135 |
| 9 | TheScrasse | 134 |
| 10 | chromate00 | 133 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2026 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 21.04.2026 07:30:18 (f1).
Десктопная версия, переключиться на мобильную.
При поддержке
C(N, K) = N! / (K! * (N — K)!) => C(N + 1, K) = C(N, K) * (N + 1) / (N + 1 — K), that's obvious.
I think, you don't know how to perform the division, so please read about modular multiplicative inverse.
You can divide by x over a prime modulus M by multiplying by xM - 2. This lets you use factorial formula for n choose k.
Well, for that task you don't even need the fact that K is constant, if you precalculate all the factorials, you can answer the nCk query in logarithmic time.
Won't you answer the query in O(1) time then?
Nope, you will need to calculate modular inverse(O(logN)).
Actually, you can calculate modular inverse O(1) with O(n) pre-calculate.
Let rv[x] is the inverse of x under M, then rv[x] = rv[M % x] * (M — M / x) % M and of course rv[1] = 1.
That's awesome!! I'm eager to know why it works. Would you explain please?
let M = kx + r, r < x, then k = M / x, r = M % x and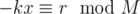
both multiple rv[x] we will get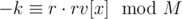
so,