Здравствуйте. Пришла в голову идея для задачи.
Вася учится в школе. Учителя ставят ему оценки от 1 до 10. Скоро настанет день, когда учителя будут вычислять квартальный балл для каждого ученика. Вся очень принципиальный человек, поэтому он хочет, чтобы его квартальный балл был ровно M. Вася заглянул в журнал и увидел, что у него уже есть N оценок, каждая из которых в диапазоне от 1 до 10. Вася не хочет часто отвечать и получать много оценок, помогите ему понять, сколько раз ему нужно ответить и какие именно оценки получить, чтобы его принцип не был нарушен.
Входные данные: В первом пряду — N и M — количество оценок и нужный ему квартальный балл. Во втором ряду записаны N оценок, от 1 до 10. Выходные данные: В первом ряду — минимальное количество оценок X . Во втором ряду — X оценок, порядок не имеет значения.
Квартальный балл вычисляется таким образом — все оценки суммируются и эта сумма делится на количество оценок. Если ответа нет — выведите -1.
Пример 1. Вход
5 5
1 5 9 7 2
Выход
1
6
Пример 2. Вход
3 8
1 2 3
Выход
9
10 10 10 10 10 10 10 10 10
Предлагайте свои методы решения и, что самое важное — предлагайте в каких диапазонах должен быть N, чтобы гарантированно уложиться в 1-3 секунды. В корректности тестов почти уверен
для первого сэмпла ответ :
Спасибо. Исправил.
второй сэмпл так же не верен! 86/11 != 8.
Там нужно 9 десяток.
да-да!
Черт. Вроде бы правильно рассчитал! Извиняюсь, сейчас найду ошибку.
Найдите еще одного такого недотепу, у которого 1+2+3 = 8 :D
За O(input + output). Решение — почти формула.
output порядка N·10, значит N < 105
Решается просто формулой. Пусть сумма имеющихся оценок равна s. Почти очевидно, что нужно набрать много десяток и взять одно число, чтобы нивелировать остаток. Пусть мы берем p десяток и число x. Тогда формула такая: s+10p+x=(n+p+1)m или s+10p=(n+p)m, если x=0. Дальше у нас либо p(10-m)+x=(n+1)m-s, откуда p=[((n+1)m-s)/(10-m)], x=(n+1)m-s-p(10-m). Либо во втором случае еще проще: p=(nm-s)/(10-m). Выдать либо первый случай, либо минимум, если во втором целое. Все. Поправьте, если вру.
UPD. Немного вру. Как раз первый сэмпл дает такой случай, когда у нас в уравнении ap+x=b правая часть меньше десяти. Тогда нужно отвечать p=0,x=b. Может, где-то еще что-то упустил =)
Is the final mark rounded down?
Nope, no rounds. If the answer can't be reached — we should output -1.
переберем ответ(сколько оценок будет в итоге). Пусть InitSum — изначальная сумма, cnt — кандидат на ответ. тогда имеем равенство (InitSum + Sum) / cnt == M; преобразуем и получаем Sum == cnt * M — initSum, тогда если мы можем набраь сумму Sum с помощью cnt — n оценок, то вот он ответ.
код
1) Можно не выводить(и не вводить, кстати — нам же только сумма и количество нужны) сами оценки — тогда можно обязать решить быстрее, чем
Unable to parse markup [type=CF_TEX]
2) Диапазон оценок выставить [1..L]
Тогда неплохая задача для Cдив2.
P.S. А кто-нибудь умеет просто и красиво решать в случае, когда оценки берутся из диапазона [S..L]? А то у меня все идеи с какими-то дикими разборами случаев.
Кстати, если оценки лежат в диапазоне, то ответ не всегда существует даже. Например, диапазон [2;3], n=2, m=2, a={2,3}. Думаю, тут без разбора случаев никак...
Ну понятно, что если m — нижняя или верхняя из диапазона оценок, то нужна проверка на существование даже в задаче из поста(n=1, m=1, a = {2}). Другое дело, что, когда оценки из диапазона [s,l], может получиться случай, когда невозможно набрать за k оценок число, лежащее в [ks, kl]. Если не ошибаюсь, плохой случай возможен при k < l и именно этот разбор случаев мне не нравится.
А почему нельзя просто из всего ввода вычесть S - 1 и свести задачу к предыдущей?
A solution.
If we can do it with x extra marks, we can also do it with x + 1 extra marks by adding another mark of value M. So we can binary search on X. A value of X is valid iff S + X - N ≤ X·M ≤ S + 10(X - N), where S is the sum of the first N marks.
You should hold on to problems like these -- maybe you can use them in a contest some day.
Well, if you have M equal to 10, but some of your current marks are different than 10, you can just take an "infinite" number of 10s and this limit goes to 10, because you have something like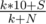
, where "S" is the sum of your marks in the beginning and k goes to infinity.
Now suppose you get k more marks, then you need to satisfy the following condition: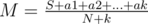
, so you need M * (N + k) to be an integer. Suppose you find the smallest k such that the mentioned experssion is an integer, now you just need a1 + a2 + ... + ak = M * (N + k) - S. This can only be satisfied when M * (N + k) - S is bigger than k and smaller than 10 * k. If it satisfies the condition, then you found your solution. If it doesn't, then you should find the next k, and because M < 10 we will once reach a k such that the conditions above are satisfied. This seems to be correct, but I'm not totally sure.
Yep, I came with the same formula when solving. I think there is a solution what computes k directly, without trying more values on it. By the way, like it was said before
a1+a2+a3+..+akis alsoX*10+Z, so we may try to play with this statement to compute k directly. And, of course, in case we can't reach M — we output -1. We can't also reach 1 if n>0 and the sum of known marks is bigger than 1.