Разбор задач Codeforces Beta Round #70 (Div. 2)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

A. Нужно было три раза подсчитать количество гласных букв в трех строках. Затем сравнить то, что получилось, с числами 5, 7 и 5. Если все совпало - вывести YES, иначе вывести NO.

Автор задачи - Ripatti.

B. Сначала можно было [n / 7] раз вывести строку ROYGBIV ([] - это округление вниз). А затем в зависимости от остатка при делении n на 7, вывести одну из следующих строк: "", "G", "GB", "YGB", "YGBI", "OYGBI", "OYGBIV". Полученная строка будет удовлетворять условию задачи.

Так же возможны другие способы построения искомой строки. Например, небольшой перебор или генерация случайных строк до тех пор, пока не найдется подходящая.

Автор задачи - Ripatti.

C. Если n четно, то всегда выигрывает Марсель - он просто симметрично повторяет ходы Тимура.

Теперь рассмотрим случай, когда n нечетно. Если Тимур не может сделать хода - он проигрывает автоматически. Если же он может сделать ход, то он всегда может разгрызть одно из бревен так, чтобы далее его части нельзя было разгрызть на меньшие части. Чтобы это сделать, нужно найти наименьшее число t такое, что k ≤ t < m и t|m, и разгрызть бревно на части длины t. После этого Тимур симметрично повторяет ходы Марселя и выигрывает.

Чтобы проверить может ли Тимур сделать ход, нужно перебрать все делители m. Если хоть для одного из них (предположим, t), выполняется k ≤ t < m, то ход сделать возможно. Проверку всех делителей можно сделать за время 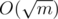$\text{[math]}$ .

Автор задачи - Lepetrandr.

D. Подобно классической задаче с подсчетом количества квадратиков в круге, данная задача решается аккуратный обходом ячеек по окружности. Сначала от центра круга будем подниматься вверх и найдем самый верхний шестиугольник, который помещается в круг. Затем сместимся на один шестиугольник вправо и вверх и от него будем двигаться вниз, пока не найдем шестиугольник, лежащий в круге. Так будем повторять до тех пор, пока не дойдем до правого края круга.

В процессе выполнения вышеописанного алгоритма к ответу будем прибавлять высоты столбиков шестиугольников. Нетрудно понять, что мы в итоге затратим O(n) времени.

О реализации. Все интересующие нас точки имеют координаты вида 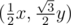$\text{[math]}$ . Поэтому расстояние до центра координат можно (и нужно) считать в целых числах. Например, проверка на то, что точка 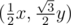$\text{[math]}$ лежит внутри круга радиуса R имеет вид x² + 3y² ≤ 4R².

Эту задачу также можно было решить за 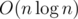$\text{[math]}$ . Просто для каждого столбика шестиугольников двоичным поиском найдем сколько шестиугольников в нем помещается в круг.

Автор задачи - Ripatti.

E. Сначала посчитаем несложную динамику от 5 параметров dp[t][x0][y0][x][y]. В каждой ячейке данной динамики будет стоять true если в момент t какой-нибудь ученый из начального блока (x0 y0) может добраться в блок (x y). В процессе пересчета данной динамики нужно учитывать распространение охлаждающей жидкости.

Теперь построим граф, состоящий из 4 частей: исток (1 вершина), первая доля (n × n вершин), вторая дола (тоже n × n вершин) и сток (1 вершина). Каждой вершине каждой доли соответствует один из блоков. От истока к первой доле проведем ребра с пропускными способностями, равными количеству ученых в соответствующих блоках. От второй доли к стоку проведем ребра с пропускными способностями, равными количеству спасательных капсул в соответствующих блоках. Из первой доли во вторую проведем ребра бесконечной пропускной способности если согласно dp ученый за время до взрыва из соответствующего блока первой доли может добраться до соответствующего блока второй доли.

Теперь в полученном графе найдем максимальный поток - он и будет ответом на задачу.

Решение имеет сложность O(tn⁴ + kn⁶), где k - максимальное количество ученых в одной клетке (в данной задаче оно равно 9).

Автор задачи - Ripatti.

Комментарии (43)

Показать архивные | Написать комментарий?

lijunle

14 лет назад, # |

where is the english version?

→ Ответить

Arkadiy

Посчитал сложность в E. У меня никак больше O(k*n^4) не получается (сложность нахождения потока грубой оценкой).

Ripatti

14 лет назад, # ^ |

Сложность тупого потока - E*F, где E - число ребер, F - размер потока. Ребер до n⁴, размер потока - kn². Отсюда kn⁶.

Ага, понятно.

ifsmirnov

Ищем поток диницей за e*sqrt(v). v = O(n*n), e = O(n^4). У меня вообще O(n^5) вышло, а от k ничего не зависит. Может автор разбора предлагал искать поток с помощью ФФ/ЭК?

2222	14 лет назад, # ^ \| 0 А как искать поток диницей за e*sqrt(v) ? → Ответить

-8

Диница ищет поток за e*sqrt(v) на графах, в которых у каждой вершины либо исходящее, либо входящее ребро единственно. Правда, я не помню, надо ли требовать, чтобы при этом все ребра имели вес 1.

_jte_

Да, должна быть единичная сеть

Tranvick

Немного оффтоп... Диниц - самый быстрый алгоритм поиска потока или есть лучше?

nk.karpov

← Rev. 2 →

Самый известный и быстрый это метод проталкивания потока(CLRS), но наверника придумали быстрее

Который за куб? Диниц может выдавать

, на разряженных графах это видимо лучше(Вот первоисточник)

Ну, а кто будет на контесте писать деревья Тарьяна ? ;)

Диница конечно хорош при поиске паросочетания(Хопкрофт-Карп).

P.S. Я имел ввиду те, которые можно написать на контесте.

Ну мало ли кто напишет =) Спасибо за ликбез

На самом деле если добавить ещё пару оптимизаций в проталкивание типа HighLevel(брать вершину с наибольшим уровнем) и GlobalRelabeling(иногда пересчитывать функцию высот bfs-ом из стока) то получается что-то неприлично быстрое

kasyankrak

Судя по оценке в описании, и по времени открытия (1997 - самый ~~модный~~ новый) может быть ЭТОТ? - )

philolo1

+14

For problem B it is also possible to use a randomiszed algorithm

do
{
randomsolution=randomCalc();

}while(!isValid(randomsolution));

DimaPhil

-15

Спасибо за разбор и контест! Задачки очень понравились. Побольше бы таких контестов!

yeputons

У кого-то, по ходу, персональный минусятор :)

ballon

Просто всех задалбывают люди коментирующие каждый новий комент ради вклада :)

khanhptnk

Please fix typing e

CosmoRied

Please elaborate on problem D, i found that counting hexagons easy initially, but as N gets bigger, my answer fails. I think I misunderstood the question even after reading it several times... For example, I don't completely understand this clarification: Then we move to the right and up from this hexagon, and then go down until we find hexagon lying inside the circle. Repeat this process until you reach the rightmost part of the circle.

-dp-	14 лет назад, # ^ \| ← Rev. 2 → +3 → Ответить

denys.astanin

I have TLE on Java with this solution. Does it actually fits to time?

? Why didn't it post? Can you tell me how to get (x, y) co-ordinate as the board is hexagonal?

← Rev. 3 →

-dp-

I think you didn't get the main idea. I've updated my picture, hope it's more clear now. We do not need to check white hexagons, only red and green ones. So, total number of hexagons we need to check is O(R). This solution easily fits to time even on Python, and on C++ it works 60ms.

Thanks for editing. But what next? We got some hexagons, but still can not say how many hexagons inside this quarter of circle. Just border hexagons. What I missunderstood?

riadwaw

We choose highest hexagon in every column.

So, we can calculate it's count

(all from highest downto - highest)in every column

oh. so easy. Thanks! :)

try to check precision.

You can write smthng like

double d1 = Math.sqrt(x1 * x1 + y1 * y1);

if (d1 > R && d1 - R > 1e-6) return false;

I_love_natalia

Мне кажется, Е гораздо проще решать вот так:
1. Флойдом ищем кратчайшие пути между вершинами (граф строим так: ИЗ реактора можно выходить, в реактор нельзя входить). Теперь для каждого ученого и каждой клетки мы знаем, может он дойти до туда или нет (ибо если ученого "перехватывает" реактор в некоторой клетке, то в конечной клетке он его тоже "перехватывает")
2. Ученых объявляем первой долей графа, выходы - второй и ищем макс-паросоч. Количество ученых и выходов не превосходит 900, на двудольном графе такого размера и достаточно регулярной структуры при реализации на матрице смежности алгоритм Куна успевает отработать (скрытая константа при кубе мала)
Учтите, я не сдавал, некогда

alexey.enkov

1. Это неверно. Например, во втором примере к задаче учёный из клетки (1, 3) успевает спастись в клетке (1, 4), хотя реактор доходит до неё за то же время (1 минута). А учёный (3, 1) не успевает спастись в клетке (4, 4), хотя тоже доходит до неё одновременно с реактором (за 4 минуты).

2. Я сам писал так же. Действительно, успевает отработать.

Согласен.
1. Ученый успевает добежать до выхода, если он там оказывается быстрее реактора, или он оказывается в соседней с выходом клетке быстрее реактора и в клетке выхода не медленнее реактора.

Кстати, общее замечание к авторам разборов - обычно авторы разбора забывают найти самый простой способ решения задачи.

Например, в В я бы указывал в разборе все-таки жадную раскраску с исправлением, наверное.

Я обычно привожу самое простое решение из тех, которые могу строго обосновать.

-dp-	14 лет назад, # ^ \| ← Rev. 2 → +16 Самое простоe в B это вывести ROY, а потом циклить GBIV сколько влезет. → Ответить

Lepetrandr

Простота решения - понятие, вообще говоря, субъективное. Кому-то может быть проще написать более громоздкое решение потому что он уже это сто раз писал подобный код и уже привык так делать (речь уже не об этой задаче). Аналогично, и для теоретических решений (если оба сравниваемых решения корректны). Мы все мыслим по-разному )

Нет, я мог написать что-то в духе "На вкус и цвет все карандаши, конечно, разные, но, думаю, что 99.81% согласятся со мной что простейшее решение это ..., благо на высокоуровневых языках типа питона оно реализуется в три операции".
Но потом подумал что нафиг разводить тут бла-бла-бла.

не туда написал, удалить нельзя, извиняюсь

caustique

13 лет назад, # |

-6

Решал задачу Е.

На 26ом тесте выдает ответ 22 вместо 24. Уже несколько часов ищу ошибку и не могу найти.

Код тут.

Кто-нибудь может подсказать, какие подводные камни могут встретиться в этой задаче?

Примечание. Свою реализацию max_flow() проверил на другом сайте - вроде работает. Может быть, ошибка в построении графа?

Примечание 2. Тест такой:

Perlik

13 лет назад, # ^ |

Не знаю как у вас, но у меня была ошибка в том (правда, тест другой), что если ученый попадал в капсулу в момент, когда туда попадала охлаждающая, он не спасался, а должен был.

fastholf

12 лет назад, # |

For task B

res[0] = 'R';
res[1] = 'O';
res[2] = 'Y';
res[3] = 'G';
res[4] = 'B';
res[5] = 'I';
res[6] = 'V';
int n;
cin >> n;
for (int i = 7; i < n; ++i) {
    res[i] = res[i - 4];
}

works as well.

Блог пользователя Ripatti