Очередной кросспост с http://sharpc.livejournal.com/68313.html#cutid1
Сегодня на Открытом Кубке мне впервые удалось успешно применить в спортивной практике метод графического дебага, и об этой success story дальше и пойдет повествование :)
Смотреть задачу O
В задаче требуется найти, с какой скоростью (от 0 до 300 м/с) должна выстрелить пушка, направленная под углом d (от 0 до 78°), чтобы из точки (xu,yu) попасть в (xo,yo), если на снаряд действует ускорение свободного падения g и ускорение силы ветра w, либо вернуть −1, если это невозможно.
Если просто записать уравнения по x и y, придется решать квадратное уравнение по t, и можно застрять в неприятных выкладках. К счастью, достаточно воспользоваться понятием равнодействующей и повернуть мир на соответствующий угол (косинус угла после этого все равно останется положительным, что благотворно влияет на его положение в знаменателе).
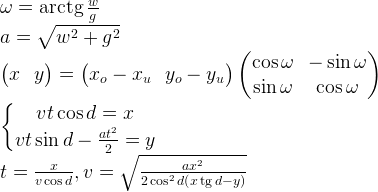
Руководствуясь этими несложными соображениями, я написал такой код с несколькими отсечениями:
И получил WA2. Самые внимательные, конечно, уже заметили ошибку, но я в их число никогда не входил и принялся дебажить :) Однако придумать подходящий тест не получилось. «А хорошо бы посмотреть для большого количества пар (x,y), как летят снаряды» — подумал я. Но стандартные средства, используемые на контестах, типа силовой отладки или логов не особо удобны для обнаружения багов в подобных задачах. Несколько удобнее была бы псевдографика, но все же она недостаточно наглядна. Хорошо бы подошел BMP, но по памяти его написать не очень просто. И тут я вспомнил о самом простом графическом формате — portable pixmap format (PPM), обнаруженном в процессе игр с AGG. Его открывают, например, XnView, Lister@Total, Photoshop. Скопирую пример из википедии:
За пару минут я написал визуализацию ответов программы на протабулированные координаты, подкрасил горизонталь, начало координат, обозначил скорость яркостью цвета, выделил среднюю скорость, и получил правдоподобно выглядящие картинки:
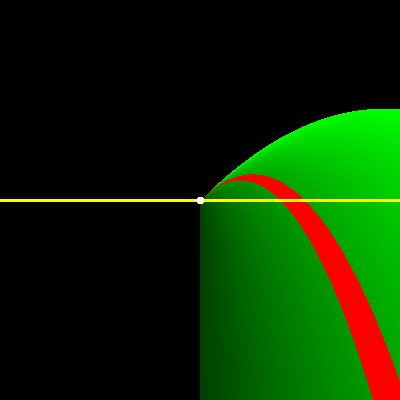
Немного поиграв с w и d, на одной из картинок я увидел странный артефакт — видимо, сработало какое-то отсечение, «испортившее» параболу:
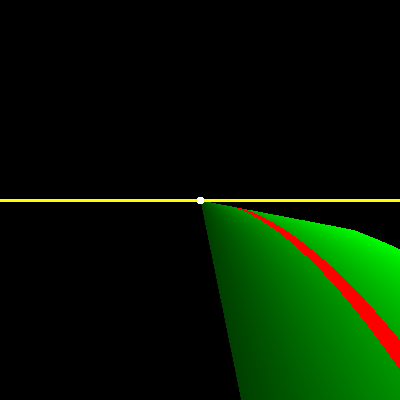
Подкрасив разные отсечения разными цветами, я нашел ошибочную строку :)
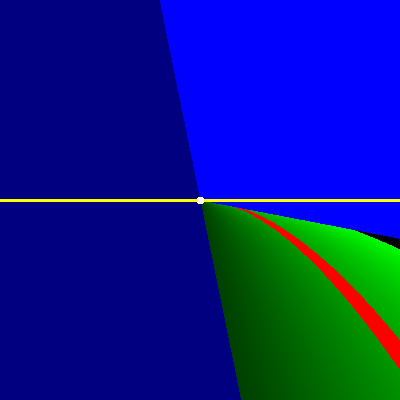
Исправил и получил AC :)
К слову, метод графического дебага, пожалуй, единственно возможный в написании рендеров. Кто видел геймдевелоперов-рендеристов за работой, тот под LSD скучает!
Сегодня на Открытом Кубке мне впервые удалось успешно применить в спортивной практике метод графического дебага, и об этой success story дальше и пойдет повествование :)
Смотреть задачу O
В задаче требуется найти, с какой скоростью (от 0 до 300 м/с) должна выстрелить пушка, направленная под углом d (от 0 до 78°), чтобы из точки (xu,yu) попасть в (xo,yo), если на снаряд действует ускорение свободного падения g и ускорение силы ветра w, либо вернуть −1, если это невозможно.
Если просто записать уравнения по x и y, придется решать квадратное уравнение по t, и можно застрять в неприятных выкладках. К счастью, достаточно воспользоваться понятием равнодействующей и повернуть мир на соответствующий угол (косинус угла после этого все равно останется положительным, что благотворно влияет на его положение в знаменателе).
Руководствуясь этими несложными соображениями, я написал такой код с несколькими отсечениями:
double solve(double x, double y, double w, double d)
{
double omega = atan(w / g);
d -= omega;
double xx = x * cos(omega) + y * sin(omega);
double yy = x * -sin(omega) + y * cos(omega);
double a = sqrt(g * g + w * w);
if (xx < 0.0) return -1;
if (xx * tan(d) <= y) return -1;
double v2 = a * xx * xx / 2.0 / (xx * tan(d) - yy) / cos(d) / cos(d);
if (v2 < 0.0) return -1;
double v = sqrt(v2);
if (v >= 0.0 && v <= 300.0) {
return v;
}
return -1;
}
{
double omega = atan(w / g);
d -= omega;
double xx = x * cos(omega) + y * sin(omega);
double yy = x * -sin(omega) + y * cos(omega);
double a = sqrt(g * g + w * w);
if (xx < 0.0) return -1;
if (xx * tan(d) <= y) return -1;
double v2 = a * xx * xx / 2.0 / (xx * tan(d) - yy) / cos(d) / cos(d);
if (v2 < 0.0) return -1;
double v = sqrt(v2);
if (v >= 0.0 && v <= 300.0) {
return v;
}
return -1;
}
И получил WA2. Самые внимательные, конечно, уже заметили ошибку, но я в их число никогда не входил и принялся дебажить :) Однако придумать подходящий тест не получилось. «А хорошо бы посмотреть для большого количества пар (x,y), как летят снаряды» — подумал я. Но стандартные средства, используемые на контестах, типа силовой отладки или логов не особо удобны для обнаружения багов в подобных задачах. Несколько удобнее была бы псевдографика, но все же она недостаточно наглядна. Хорошо бы подошел BMP, но по памяти его написать не очень просто. И тут я вспомнил о самом простом графическом формате — portable pixmap format (PPM), обнаруженном в процессе игр с AGG. Его открывают, например, XnView, Lister@Total, Photoshop. Скопирую пример из википедии:
P3
# The P3 means colors are in ASCII, then 3 columns and 2 rows,
# then 255 for max color, then RGB triplets
3 2
255
255 0 0 0 255 0 0 0 255
255 255 0 255 255 255 0 0 0
# The P3 means colors are in ASCII, then 3 columns and 2 rows,
# then 255 for max color, then RGB triplets
3 2
255
255 0 0 0 255 0 0 0 255
255 255 0 255 255 255 0 0 0
За пару минут я написал визуализацию ответов программы на протабулированные координаты, подкрасил горизонталь, начало координат, обозначил скорость яркостью цвета, выделил среднюю скорость, и получил правдоподобно выглядящие картинки:
Немного поиграв с w и d, на одной из картинок я увидел странный артефакт — видимо, сработало какое-то отсечение, «испортившее» параболу:
Подкрасив разные отсечения разными цветами, я нашел ошибочную строку :)
if (xx * tan(d) <= y) return -1;
Исправил и получил AC :)
К слову, метод графического дебага, пожалуй, единственно возможный в написании рендеров. Кто видел геймдевелоперов-рендеристов за работой, тот под LSD скучает!











UPD: Это я не понял, что именно являлось ошибкой. Попелышев прав.