akulsareen's blog

Topcoder Single Round Match 661
By akulsareen, history, 9 years ago, In English

I usually like to wait for chrome or someone else to remind all you good folk about an upcoming SRM but it seems like they have forgotten. So here goes.

Hi there!

Tomorrow at 6:30 IST will be held Topcoder SRM 661.

Let's discuss problems after contest!

GL && HF.

  • Vote: I like it
  • +73
  • Vote: I do not like it

Comments Comments (37)
| Write comment?
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone knows about the goodies, rankwise or random?

→ Reply
»
9 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Will you be able to wake up in time? :P

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Reminder for anyone who is awake but not registered. 5 minutes left till end of registration.

→ Reply
»
9 years ago, # |
  Vote: I like it +68 Vote: I do not like it

Congratulations to Swistakk on finally getting into top5 :)

BTW, can someone please explain where does that magic formula for div1 450 come from?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +58 Vote: I do not like it

    if you mean i(k — 1) + 1 then i can explain : we either take no edges for the i'th node then we can color it with k colors else we can take either of the (i-1) edges and since this nodes color can't be the same as the node where the edge is pointing we can color it with k — 1 colors thus it's (k-1)(i-1) + k = i(k-1) + 1

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +34 Vote: I do not like it

      Thanks... Now after your explanation it sounds so obvious and easy)

      And I had to write a brute force to get the formula :(

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        you're welcome xD it took a time for me to get it that's why i couldn't complete it :((

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +13 Vote: I do not like it

        Yeah, similar situation here too. I came to a formula thas was wrong, coded it, forgot to add a couple of lines and it magically worked (yeah, coding it wrong fixed the formula). I was really lucky there.

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Daaaamn. Just noticed that we had to pick only one edge. I was making a formula thinking if at the ith node I have degree 0, or degree 1, or degree 2.... to get a recurrence with binomial coefficients in it.

      Is my misread version of the problem solvable?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        sounds pretty damn hard

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        i noticed it just after seeing your comment :(

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          to Sumeet.Varma and akulsareen:

          it's always better if you check that you completely understand the samples before you start thinking of the problem, even if you think your self that you understand the problem completely

          I learnt that lesson after one of my previous contest I participated

          → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can somebody tell me what is the problem with this code for Div1 450? Thanks in advance!

      int ColorfulLineGraphs::countWays(long long N, long long K, int M)
{
ll ans,term,times,start,end,y;
ans = 1;
for (int i=0; i<M; i++) 
{
	y=((i==0)?M:i);
	start = y;			// smallest x (1<=x<=N) such that x%M = i
	end = N/y*y;			// largest x (1<=x<=N) such that x%M = i
	if(end>=start)
	{
		term = (i * (K-1) + 1) % M;
		times = (end - start)/M + 1;	// how many x (1<=x<=N) such that x%M = i
		ans =(ans * power( term, times, M ) )%M; // (term^times) modulo M
	}
}
return ans;
}
      → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +152 Vote: I do not like it

    Congratulations to Swistakk on finally getting into top5 :)

    Plot twist: Petr forget to cover today's SRM

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Whats your handle on TC?

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve Div2 500?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Since constraint is only 11, we can simply iterate over all possible combinations of bridges to build and then run a Floyd-Warshall on each of them to find the diameter. (By finding max of distance between 2 nodes)

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You have to choose k elements out of n elements(k <= n);

    So iterate from 0 to (1 << n), if number of set bits is equal to k , use all pair shortest path(floyd-warshall).

    My implementation of Floyd was wrong which made me nervous and I could not complete in Time.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

950 < 500 < 250

Div-2 contestants will understand -_-

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    Well, I did solve only 1000 in div1 :D (why did I have to misread 250...)

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it +3 Vote: I do not like it

      Positions of guys who have solved 1000 — 1, 2, 3, 4 and 63 xD

      → Reply
»
9 years ago, # |
  Vote: I like it +2 Vote: I do not like it

How to solve div2 1000? Was there some magic formula there?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Imagine that you are constructing the same graphs but in a different way: for each i between 1 and N, inclusive, you:

    1. choose whether you want an edge from node i
    2. if you do want it, choose where it points (i-1 possibilities)
    3. color the node (K possibilities if you didn't draw an edge, K-1 if you did)
    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Now I think I should have spent a little more time on the 1000(in today's case 950) rather than the 500. :(

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Okay, so for some i<=n, shouldn't the correct relation be

      ans = ans * (k + (k-1)*(i-1)*k) ?

      Where the second term means : Colour the current value in k ways, and have i-1 possible edges leading to k-1 different colours?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        no the recurrence is something like

        f(1) = K, as we can choose one node with colour 1, 2, ..., K

        f(n) = K*f(n-1) + (n-1)*(K-1)*f(n-1)

        the first term is translation to: put the n-th node on the right side of the f(n-1) old graphs choosing its colour to be 1, 2, ..., K

        and about the (k-1)*f(n-1) it is about: for some i in the range 1<= i <=n-1 (so there is (n-1) such i) put the n-th node and connect it with an edge to this i-th node we can do that only if n-th colour is different from i-th colour which allows to choose (K-1) colour

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Yes, but regarding the second term, Shouldn't you select the current element's colour in K ways, and the for each of these colours, an edge which leads to the n-1 elements each with k-1 colours?

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            yes I understand what you mean, the approach written above is about another approach from what you are thinking. In my opinion it is simpler. However if you want to solve it considering the idea you have, you have to change the definition of f(n), for the approach above f(n) = the number of graphs that can be constructed in the way mentioned in the problem statement (and have n nodes) using all K colours. Maybe for your approach you have to define something like f(n, m) = the number of graphs that can be constructed in the way mentioned in the problem statement (and have n nodes) using m colours or something else.

            → Reply
»
9 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Approach to solve Div1 250 plaease?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Since LCM(N + 1..M)|LCM(1..M) (think why) and LCM is the product of maximum prime powers dividing some number in the respective ranges, you only need M large enough for any pk that divides some number  ≤ N (i.e. any pk ≤ N, but you don't need this) to divide also some number x between N + 1 and M (the smallest such x), so M is the maximum of these x. Therefore, you just need to factorise all numbers up to N by the sieve of Erathostenes.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Btw, Can you prove that in fact we only need to consider pk -  > 2pk and that all cases xpk -  > (x + 1)pk are not needed? It is sufficient to prove that there is any power in an interval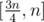 and that is in fact true even for just primes (maybe for sufficiently large n's), but it's some freaking hard math xd.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Hmm idk, but I can finally prove that a non-constant polynomial has at least one root :D. Complex calculus is weird in many ways.

        → Reply