Простая задача, которая проверяет знание матана 1 курса.
Пусть-- достаточно гладкая функция, которая определена на отрезке от 0 до 3.
Известно, что.
Докажите, что.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
20:07:20
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
20:07:20
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 21:27:41 (j1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Разложим функцию в ряд Фурье на [0..3], учитывая, что f(0) = f(3) = 0 и воспользуемся равенством Парсеваля
т.к , то получаем, что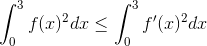
В СУНЦ МГУ проходят в 10 классе.Так что где-то, наверное, и на 1 курсе проходят.
Я буду перечитывать, на что я отвечаю.
Я буду перечитывать, на что я отвечаю.
Я буду перечитывать, на что я отвечаю.
Убейте меня, прочитал "Фурье" как "Тейлора".
Возьмем функцию, удовлетворяющуюю нашему условию - f(x)=x*(x-3)
Найдем производную f'(x)=2x-3.
Далее, перенесем левый интеграл вправо и возьмем обе функции под один интеграл. Далее, возведем обе функции в квадрат, приведем подобные и получим:
0<=Интеграл(-x^4+6x^3-5x^2-12x+9)dx.
Взяв интеграл от 0 до 3, получил положительное число 18,9. Значит равенство верно.
Мы можем взять любые функции, то т.к. мы их возводим в квадрат, то их значения всегда будут положительными, следовательно мы всегда получим, что интеграл разности квадратов этих функций будет положителен.
Следовательно, у вас ошибка.
Надо как-то использовать такую штуку, что интеграл от f '(x) от 0 до 3 равен нулю. Может как-то по частям разложить данные интегралы? Что-то обнулится и мы получим, что площадь некоторой функции больше нуля. Только нужно преобразовать.
Это правильное начало?
А изменится ли что-то, если число 0 заменить числом a, а число 3, заменить числом b в пределах интегрирования и указать, что f(a)=f(b)=0. И все оставить как прежде.
Или это важно, что в условии именно числа 0 и 3?
Изменение b-a характеризует всего лишь сжатие или расширение этого отрезка. Определенный интеграл - площадь под графиком функции, которая при сжатии или расширении фигуры просто пропорционально уменьшается или увеличивается. Так что неравенство не изменится.
Где ошибка?
Во-первых, пример некорректный, т.к. sin(4) != 0
Во-вторых? неравенство верно: <формул больше нет>
фурье там не проходил из-за недостаточной гладкости