Hi everbody! Well, I've been trying to understand the solution for this problem for a while, but I think I need a little help.
Solutions (all SWERC 2012): http://users.dsic.upv.es/swerc_12/ProblemSet2012/SWERC-2012-solution-outlines.pdf
Yes, it has a pdf with the solution explained. The thing is that there is a mistake (or I can not understand what they mean). They talk about a function SOD(x), which is Sum Of Divisors of x. But the SOD of 12, for example, clearly isn't 3, as they say in the pdf.
I hope someone can give me a hand with it, and if you have some extra topics I can read about, that might help me with this problem, would be great as well!
Thanks in advance.











The second column in the table means sum of divisors of the number p1a1·p2a2·...·pcac, if Qi = p1a1 + 1·p2a2 + 1·...·pcac + 1
Thank you for you answer, now I understand at least what they do in the tutorial. But anyway, I still can not figure out why that solve the problem. I mean, why that function calculates the correct answer... is there some theorem I'm missing or just logic?
A few transformations:
Let h(n) = f(n) - n, and as ffao hinted, it's a good time to notice that h(n) is multiplicative. Now let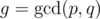 and replace p and q with gp and gq, making p and q relatively prime:
and replace p and q with gp and gq, making p and q relatively prime:
Let's split n into two divisors d and n / d,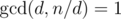 (so they have factors Qi and Ri in the official solution). Group q by having the same set of prime factors as d, then p will divide n / d:
(so they have factors Qi and Ri in the official solution). Group q by having the same set of prime factors as d, then p will divide n / d:
The last sum is the number of divisors of n / d. Replace q with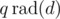 :
:
Apply this equation: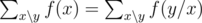 .
.
which is about the same expression as in the solution.
This problem is funny because it has a solution in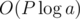 , which is way easier to code than the intended solution in O(2P). I guess they just didn't see it.
, which is way easier to code than the intended solution in O(2P). I guess they just didn't see it.
Hint: if you know f(p1a1) and f(p2a2), is there an easy way to get f(p1a1p2a2)?