Hello, I've been trying to learn new useful data structures, I've tried to implement a couple "sqrt descomposition" problems lately. I came across this problem a couple of weeks ago: http://coj.uci.cu/24h/problem.xhtml?pid=3228. The problem statement is pretty simple and straight to the point. I think I came up with a O( sqrt(N) * log(N) ) solution which might work: http://ideone.com/ibCkwY. But, I keep getting a TLE veredict. Is there a faster approach with Segment Tree or any other data structure? or even a better way to solve this one with Sqrt Descomposition?
Thank for reading, Any kind of help is appreciated











all below is incorrect
Treap might solve this problem.You can split tree on the 3 parts by indecies L and R. After that split second part by value X on the 2 parts where size of first part will be the answer. And finally merge all parts back.
I am not familiar with a Treap. Did you try to submit a solution with this approach that you ruled out it as a possible solution ?
It's a classical problem about 2D data structures, can be solved with 2D segment tree + compaction in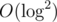 per query.
per query.
Could you please elaborate a little bit more on this solution? I am not familiar with 2D data structures and there are no many useful articles regarding this topic. As far as I know the 2D Segment Tree takes about O(n×m) memory which should get a MLE veredict. Even if I compress the values using a map or something a lot of memory is going to be used.
That memory consumption is correct for 2D BIT or naive implementations of 2D segment tree.
However, you can optimize 2D segment tree to take memory (here n stands to amount of different points in that tree. To do that, you should compress coordinates not once in the beginning, but on each level of the outer segment tree. That way, if some inner segment tree stores k points, it will take O(k) memory, not O(MAXCOORD).
memory (here n stands to amount of different points in that tree. To do that, you should compress coordinates not once in the beginning, but on each level of the outer segment tree. That way, if some inner segment tree stores k points, it will take O(k) memory, not O(MAXCOORD).
I did it in that way with sqrt decomposition, it get AC with O(sqrt(N) * log(sqrt(N))) per query.
This problem should be solvable in O((N + Q) log^2 N) using Segment Tree with an Order Statistic Tree at each node.
Each node of the segment tree responsible for the range (S, E) will store an Order Statistic Tree containing all the numbers currently in the range (S, E).
For each update, you update each node recursively up the Segment Tree by removing the old value from every Order Statistic Tree and inserting the new value. For each query, you find the number of numbers less than X in each Order Statistic Tree that corresponds to the queried range, using the Segment Tree.
Since each delete(), insert() and query() operation on the Order Statistic Tree takes O(log N) and there are at most O(log N) Order Statistic Trees to query or update, this algorithm will take O((N + Q) log^2 N) overall.
P.S. An implementation of the Order Statistic Tree in C++ is Policy-Based Data Structure (PBDS).
Can be solved with merge sort tree with pbds on each vertex https://mirror.codeforces.com/blog/entry/11080