Given two integers N and M, count the number of integers x between 2 and N! , having the property that all prime factors of x are greater than M. Where 1≤M≤N<10000001 and (N-M)≤100000. Can anyone help me with the logic?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
34:47:34
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
34:47:34
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 06:47:26 (l1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Use "sieve of eratosthenes" and find prime numbers that is greater than M and smaller than N all the numbers we want is multiplication of these prime number.
Well but i think it's not possible to find the prime numbers till N!.(N factorial)
I think you can calculate instead the count of numbers that have prime factors smaller than M in the range 2 to N! and substract it from N! - 1. Now let the primes smaller than M pe p1, ..., pk, then by simple inclusion, exclusion the quantitiy you want is equal to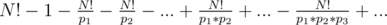 which is similar to euler's toitient function formula and you can write it as
which is similar to euler's toitient function formula and you can write it as 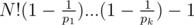 .
.
I hope this is correct.
can you post the link of this problem?
I think there's no way to solve this problem right now. Since U need to find all the prime numbered from M to N!. Let the count be X, our answer is 2^X -1.
Here is the problem link : https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=2435