ironman7453's blog

Maximum Longest Increasing Subsequence
By ironman7453, history, 9 years ago, In English

I am trying to solve this problem, but so far no luck. Can anybody show me the correct approach. I know that it is possible to find longest increasing subsequence in O(n2) time using dp.

Problem statement:

Given a sequence of integers, find the maximum difference between first and last element of the longest increasing subsequence.

Input:

First line contains T, number of test cases followed by T test cases. For each test case first line contains an integer N , the next line contains sequence of N integers.

Constraints:

T <  = 100

1 <  = N <  = 10000

All numbers in the sequence will fit into 64-bit integer

  • Vote: I like it
  • +1
  • Vote: I do not like it

Comments Comments (9)
| Write comment?
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For this problem, we can do the same thing we do in a lis nlogn. Make a lis O(nlogn) with a set and save the predecessors of positions that you insert in your set. After that, you have a complete sequence of lis. You can store de id's of the positions and after that, you can discover the maximal difference between first and last number. Be careful that possible overflows! :)

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    Yeah I just found the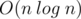 algorithm for finding longest increasing subsequence. But there maybe multiple such subsequences. How can I find all such subsequences?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      You not need test all the subsequences. You need construct the increasing subsequence that the start is the lowest possible. Imagine that the "final lis" have length X. If you can make a lis that the length is X-1 , you can try find the last element in linear time. Obviously, do you take the maximum element possible.

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My implementation O(nlogn): http://pastebin.com/L1SW8Jf9

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    Unfortunately it gives TLE.

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The question previously had strict time limits ; and gave TLE even on correct implementations ; now the solution provided by you is not getting TLE ; although it still receives a WA.

    Even I tried to submit the code ; but I also got WA ; and not a single submission is AC on the problem...

    Maybe test cases are wrong or something like that...

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      Update : No ; the code fails on array — 10 20 30 15 20

      There are two possible candidates for LIS :

      1. ( 10 , 20 , 30 )
      2. ( 10 , 15 , 20 )

      ans = max ( 30-10 , 20-10 ) = 20 Code outputs 10

      → Reply
      • »
        »
        »
        »
        2 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I wrote a code with a segment tree but I'm still getting WA. The funny about this problem is that no one solved it according to the search filter of the submissions.

        Consider this example: $$$100 20 30 5$$$

        First step:

        Compress the numbers range (compress coordinates), i.e. $$$100 20 30 5$$$ becomes $$$4 2 3 1$$$ so we will have numbers at most between $$$1$$$ and $$$n$$$. This should work because we only care who they are relative to each other. We should get the same max length of an increasing subsequence.

        Second step:

        Start at the first number $$$a_1$$$ and use a segment tree to update lasily the range $$$[a_1, n]$$$ with the length of and the tail (smallest number). Each number will be updated lasily if it gives a maximal answer if we updated it.

        Code
        → Reply
»
9 years ago, # |
  Vote: I like it -11 Vote: I do not like it

Watch this video for O(n^2) solution then watch this video for O(n log n) solution

→ Reply