I have been trying to solve this problem.
We need to find the ($$$N+1-K)^{th}$$$ coefficient of the polynomial $$$(x+N)(x+N+1)(x+N+2)...(x+M-1)(x+M)$$$.
When $$$K=3$$$, $$$C(N,M,K)$$$ can be easily calculated by the triple sum $$$\sum_{a=N}^{M}\sum_{b=a+1}^{M}\sum_{c=b+1}^{M}abc$$$
As $$$K$$$ becomes larger, finding closed form of the sum becomes difficult. I tried another approach. When $$$M-N$$$ and $$$K$$$ are fixed, $$$C(N,M,K)$$$ can be expressed as a polynomial of degree $$$K$$$ on the variable $$$N$$$.
For example, if $$$M-N=10$$$ and $$$K=3$$$, $$$C(N,N+10,3)=18150+11880N+2475N^2+165N^3$$$.
Final answer should be a polynomial of degree $$$50$$$. But to find the coefficients, I need $$$50$$$ data points. So far I have been unable to evaluate those. Any help will be much appreciated.
P.S. — This problem is not from an ongoing competition.









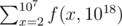 mod
mod 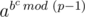 mod
mod 
