ironman7453's blog

Number Theory Problem
By ironman7453, history, 9 years ago, In English

I found the following problem here.

f(x, n) = x21 + x22 + x23 + ... + x2n

Example: f(2, 10) mod 1000000007 = 180974681

Calculate 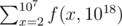mod 1000000007.

We know that abc mod p = 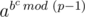mod p.

The period of the sequence 2n mod 1000000006 is φ(1000000006) = 500000002.

The period is too large to calculate the sum. Help please?

  • Vote: I like it
  • +14
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +16 Vote: I do not like it

Let q = 5·108 + 3 and p = 2q + 1.

As 1018 = 1999999992(q - 1) + 16 we have

f(x, 1018) = (x2 + x4 + ... + x2q - 2)·1999999992 + x2 + ... + x216 =  - 1·1999999992 + x2 + ... + x216.

We used the fact that 2 is a primitive root modulo q and that

So we just have to compute 107·16 values which should be fine.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    Unfortunately I am not getting the correct answer using this approach. I am getting the answer 224649977, which is incorrect. Here is my code:

    import java.io.*;
import java.util.*;
import java.math.*;

public class sol {
    public static long mod = 1000000007L;
    public static long phi = 1000000006L;
    public static BigInteger MOD = new BigInteger("1000000007");
    public static BigInteger PHI = new BigInteger("1000000006");
    public static BigInteger a2 = new BigInteger("2");
    public static BigInteger b = new BigInteger("22"); // -1999999992 mod 1000000007
    public static ArrayList<BigInteger> pow = new ArrayList<BigInteger>();
    public static void main(String[] args) throws IOException {
	double start = System.currentTimeMillis();
        long p = 2L;
        for (int i = 1; i <= 16; i++) {
            pow.add(BigInteger.valueOf(p));
            p *= 2L;
        }
        //System.out.println(pow);
        long res = 0L;
        for (long x = 2L; x <= 10000000L; x++) {
            if (x % 100000 == 0) System.out.println(x / 100000);
            long t = g(x);
            res += x;
            res %= mod;
        }
        if (res < 0) {
            res += mod;
        }
        System.out.println(res);
        double end = System.currentTimeMillis();
	System.out.println("Time elapsed : " + ((end - start) / 1000d) + " seconds");
    }

    public static long g(long x) {
        BigInteger X = BigInteger.valueOf(x);
        BigInteger sum = BigInteger.valueOf(0);
        for (BigInteger p : pow) {
            sum = sum.add(X.modPow(p, MOD));
        }
        sum = sum.add(b);
        sum = sum.mod(MOD);
        return sum.longValue();
    }
}
    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      I guess you have a bug here:
      Try instead of:

      res += x;

      put

      res += t;

      Well, and we don't have to use BigIntegers. We can compute those powers by simple squaring the previous one. The answer can be returned in ~1 second if we implement this in an efficient way.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Ohh, -_- What a silly mistake. I implemented using long. I thought I had overflow error. Sorry. Thanks again.

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
          ← Rev. 4   Vote: I like it +3 Vote: I do not like it

          I calculated 1k + 2k + ... + nk using Faulhaber's formula for k = 21, 22, ..., 216, but it still takes 1 minute. How can I improve it?

          EDIT: Ok, I made significant improvement. Now it runs in 3.85 seconds. How can I make it faster? Below is my code:

          import java.io.*;
import java.util.*;
import java.math.*;

public class sol {
    public static long mod = 1000000007L;
    public static void main(String[] args) throws IOException {
        double start = System.currentTimeMillis();
        long N = 10000000L;
        long res = 21L * N;
        for (long n = 2L; n <= N; n++) {
            res += f(n);
            res %= mod;
        }
        System.out.println(res);
        double end = System.currentTimeMillis();
	System.out.println("Time elapsed : " + ((end - start) / 1000d) + " seconds");
    }

    public static long f(long n) {
        long t = n * n % mod;
        long s = t;
        for (int i = 1; i < 16; i++) {
            t = t * t % mod;
            s += t;
            s %= mod;
        }
        if (s < 0) {
            s += mod;
        }
        return s;
    }
}
          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Why do you need it faster? On project Gauss you can spend as much time as you want on computing the answer. It is not necessary that there is always fast, e.g. 1 second solution.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              9 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Learning faster solutions maybe useful in future. Anyway, I don't think above solution can be much improved. 3-4 seconds is pretty good.

              → Reply