I found the following problem here.
f(x, n) = x21 + x22 + x23 + ... + x2n
Example: f(2, 10) mod 1000000007 = 180974681
Calculate 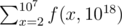 mod 1000000007.
mod 1000000007.
We know that abc mod p = 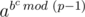 mod p.
mod p.
The period of the sequence 2n mod 1000000006 is φ(1000000006) = 500000002.
The period is too large to calculate the sum. Help please?











Let q = 5·108 + 3 and p = 2q + 1.
As 1018 = 1999999992(q - 1) + 16 we have
f(x, 1018) = (x2 + x4 + ... + x2q - 2)·1999999992 + x2 + ... + x216 = - 1·1999999992 + x2 + ... + x216.
We used the fact that 2 is a primitive root modulo q and that
So we just have to compute 107·16 values which should be fine.
Unfortunately I am not getting the correct answer using this approach. I am getting the answer 224649977, which is incorrect. Here is my code:
I guess you have a bug here:
Try instead of:
put
Well, and we don't have to use BigIntegers. We can compute those powers by simple squaring the previous one. The answer can be returned in ~1 second if we implement this in an efficient way.
Ohh, -_- What a silly mistake. I implemented using long. I thought I had overflow error. Sorry. Thanks again.
I calculated 1k + 2k + ... + nk using Faulhaber's formula for k = 21, 22, ..., 216, but it still takes 1 minute. How can I improve it?
EDIT: Ok, I made significant improvement. Now it runs in 3.85 seconds. How can I make it faster? Below is my code:
Why do you need it faster? On project Gauss you can spend as much time as you want on computing the answer. It is not necessary that there is always fast, e.g. 1 second solution.
Learning faster solutions maybe useful in future. Anyway, I don't think above solution can be much improved. 3-4 seconds is pretty good.