Um_nik's blog

Codeforces Round #315 Editorial
By Um_nik, history, 9 years ago, translation, In English

569A - Music

Suppose we have downloaded S seconds of the song and press the 'play' button. Let's find how many seconds will be downloaded when we will be forced to play the song once more. 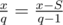. Hence x = qS.

Solution: let's multiply S by q while S < T. The answer is the amount of operations.

Complexity —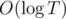

569B - Inventory

Let's look at the problem from another side: how many numbers can we leave unchanged to get permutation? It is obvious: these numbers must be from 1 to n and they are must be pairwise distinct. This condition is necessary and sufficient.

This problem can be solved with greedy algorithm. If me meet the number we have never met before and this number is between 1 and n, we will leave this number unchanged. To implement this we can use array where we will mark used numbers.

After that we will look over the array again and allocate numbers that weren't used.

Complexity — O(n).

568A - Primes or Palindromes?

It is known that amount of prime numbers non greater than n is about .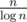

We can also found the amount of palindrome numbers with fixed length k — it is about 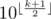which is .

Therefore the number of primes asymptotically bigger than the number of palindromic numbers and for every constant A there is an answer. Moreover, for this answer n the next condition hold: 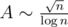. In our case n < 107.

For all numbers smaller than 107 we can check if they are primes (via sieve of Eratosthenes) and/or palindromes (via trivial algorithm or compute reverse number via dynamic approach). Then we can calculate prefix sums (π(n) and rub(n)) and find the answer using linear search.

For A ≤ 42 answer is smaller than 2·106.

Complexity — .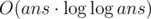

568B - Symmetric and Transitive

Let's find Johnny's mistake. It is all right in his proof except ``If 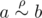'' part. What if there is no such b for an given a? Then obviously 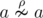otherwise we'll take b = a.

We can see that our binary relation is some equivalence relation which was expanded by some "empty" elements. For "empty" element a there is no such b that .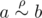

Thus we can divide our solution into two parts:

  1. Count the number of equivalence relations on sets of size 0, 1, ..., n - 1

  2. For every size count the number of ways to expand it with some "empty" elements.

We can define equivalence relation using its equivalence classes.

So first part can be solved using dynamic programming: dp[elems][classes] — the numbers of ways to divide first elems elements to classes equivalence classes. When we handle next element we can send it to one of the existing equivalence classes or we can create new class.

Let's solve second part. Consider set of size m. We have found that there are eq[m] ways to build equivalence relation on this set. We have to add n - m "empty" elements to this set. The number of ways to choose their positions is Cnk. We can calculate all the binomial coefficients using Pascal's triangle.

So the answer to the problem is .

Complexity — O(n2)

568C - New Language

Suppose we have fixed letters on some positions, how can we check is there a way to select letters on other positions to build a word from the language? The answer is 2-SAT. Let's see: for every position there is two mutually exclusive options (vowel or consonant) and the rules are consequences. Therefore we can do this check in O(n + m) time.

Let's decrease the length of the prefix which will be the same as in s. Then the next letter must be strictly greater but all the next letters can be any. We can iterate over all greater letters and then check if we can made this word the word from the language (via 2-SAT). Once we have found such possibilty we have found the right prefix of the answer. After that we can increase the length of the fixed prefix in a similar way. This solution works in O(nmΣ ) time. We can divide this by Σ simply try not all the letter but only the smallest possible vowel and the smallest possible consonant.

And you should remember about the case when all the letters are vowel (or all the letters are consonant).

Complexity — O(nm)

568D - Sign Posts

Suppose, that solution exist. In case n ≤ k we can put one signpost on each road. In other case let's choose any k + 1 roads. By the Dirichlet's principle there are at least two roads among selected, which have common signpost. Let's simple iterate over all variants with different two roads. After choosing roads a and b, we will remove all roads, intersecting with a and b in common points and reduce k in our problem. This recursive process solves the problem (if solution exist).

Complexity of this solution — 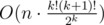. If implement this solution carefully — you will get AC =)

But in case of TL we can add one improvement to our solution. Note, that if we find point, which belongs to k + 1 or more roads, then we must include this point to out answer. For sufficiently large n (for example, if n > 30k2) this point always exist and we can find it using randomize algorithm. If solution exist, probability that two arbitrary roads are intersects in such a point not less than 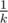. Because of it, if we 100 times pick two random roads, then with probability 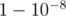such a point will be found and we can decrease k.

All operations better to do in integers.

Complexity — .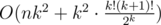

568E - Longest Increasing Subsequence

Let's calculate array c: c[len] — minimal number that can complete increasing subsequence of length len. (This is one of the common solution for LIS problem).

Elements of this array are increasing and we can add new element v to processed part of sequence as follows:

  1. find such index i that c[i] ≤ v and c[i + 1] ≥ v

  2. let c[i + 1] = v

We can process this action in time.

When we handle a gap, we must try to insert all numbers from set b. If we sort elements of b in advance, then we can move with two iterators along arrays b and c and relax all needed values as explained above. This case requires O(n + m) time.

Authors implied solution with O(n) space complexity for answer restoring. We can do this in the following way:

  1. Together with array c we will store array cindex[len] — index of element, which complete optimal increasing subsequence of length len. If this subsequence ends in a gap — we will store  - 1.

  2. Also, we will store for every not gap — length of LIS(lenLIS[pos]), which ends in this position (this is simply calculating while processing array c) and position(prevIndex[pos]) of previous element in this subsequence (if this elements is gap, we store  - 1)

Now we will start recovery the answer with this information.

While we are working with not gaps — it's all right. We can simply restore LIS with prevIndex[pos] array. The main difficulty lies in processing gaps. If value of prevIndex[pos] in current position equal to  - 1 — we know, that before this elements must be one or more gaps. And we can determine which gaps and what values from b we must put in them as follows:

Let suppose that we stand at position r (and prevIndex[r] =  - 1). Now we want to find such position l (which is not gap), that we can fill exactly lenLIS[r] - lenLIS[l] gaps between l with increasing numbers from interval (a[l]..a[r]). Position l we can simply iterates from r - 1 to 0 and with it calculating gaps between l and r. Check the condition described above we can produce via two binary search query to array b.

Few details:

  1. How do we know, that between positions l and r we can fill gaps in such a way, that out answer still the best?
    Let countSkip(l, r) — count gaps on interval (l..r), countBetween(x, y) — count different numbers from set b, lying in the range (x..y).
    Then, positions l and r are good only if lenLIS[r] - lenLIS[l] = min(countSkip(l, r), countBetween(a[l], a[r])). countSkip we can calculate while iterates position l, countBetween(x, y) = max(0, lower_bound(b, y) - upper_bound(b, x)).

  2. What to do, is LIS ends or begins in gaps?
    This case we can solve by simply adding  - ∞ and  + ∞ in begin and end of out array.

Complexity — 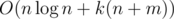. Memory — O(n + m).

  • Vote: I like it
  • +110
  • Vote: I do not like it

Comments Comments (77)
| Write comment?
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been translated by Um_nik(original revision, translated revision, compare)

→ Reply
»
9 years ago, # |
  Vote: I like it +17 Vote: I do not like it

thanks for fast editorial :)

→ Reply
»
9 years ago, # |
  Vote: I like it -42 Vote: I do not like it

"Music", worst problem I've ever seen!

→ Reply
»
9 years ago, # |
  Vote: I like it -34 Vote: I do not like it

Fast Editorial

→ Reply
»
9 years ago, # |
  Vote: I like it +10 Vote: I do not like it

For problem 568B — Symmetric and Transitive I propose an alternate view:

Let's suppose we see the relation as a graph. In essence, a-R->b will mean the edge (a,b) in our graph. Now, the properties translate to:

(u, v), (v, w) exist => (u, w) exists (transitivity) The graph is undirected (symetry) There is (u, u) for each u (reflexivity).

Now, we notice some properties: - (u, v) exists => (v, u) exists => (u, u) exists (by reflexivity and transitivity). - also by transivity, we can see that each vertice of a graph is either isolated (has no incident edges) or is part of a clique — this is important.

So, the graph is a reunion of cliques of size >= 1 plus a number of isolated vertices. Now, let's suppose that k vertices are isolated. Then n-k of them are part of the "reunion of cliques". Now, we can choose the k isolated vertices in (n choose k) ways. The rest is a reunion of cliques. Simply, every node is part of a clique (of size >= 1).

If we consider Cliques[i] -> the number of graphs that are "reunion of cliques" with i vertices, then the answer is sum(1, n-1) (n choose k) * Cliques[n-k] + 1. The "1" represents an empty graph, which was not considered earlier.

To calculate Cliques[i], we can think of every node taking part of a clique. It's easy to see why this relates to partitions. In particular, Cliques[i] is the total number of ways to partition i numbers. It is equal to S[i][1] + S[i][2] + ... + S[i][i], where S[i][j] is the 2nd Stirling's Number (i.e., the number of ways we can partition i items in j groups).

So, basically, we calculate S[i][j](Stirling), C[i][j](Combinations), and then Cliques[i] (as S[i][1] + S[i][2] + ... + S[i][i]). Now, the answer is C[n][1] * Cliques[n-1] (1 isolated node) + C[n][2] * Cliques[n-2] (2 isolated nodes) + ... + C[n][n-1] * Cliques[1] (n-1 isolated nodes) + 1 (empty graph). I hope it was clear enough, I don't know how to write explanations that well :)

→ Reply
»
9 years ago, # |
← Rev. 9   Vote: I like it +24 Vote: I do not like it

I used a different dp for computing the number of equivalence relations on a set of size n in 1B/2D: let dp[i] be the number of equivalence relations on a set of size i. While computing dp[i+1], consider a particular number (say i+1)- let's say there are x other elements belonging to the equivalence class of that number. Once we select those x numbers (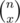 ways to do that), we have dp[i-x] possibilities for the remaining numbers, giving the recursion

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please explain "For A ≤ 42 answer is smaller than 2*10^6." for 569C - Простые или палиндромы?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What don't you understand? It is statement about maximal answer, it is true.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I ain't understand that why it is less than 2*10^6 ? My code have failed, because I have used until 10^7.

      (Sorry for my bad English)

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        We have proved that it is less than 10^7 and then found real answer.

        I can't understand your question.

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 3   Vote: I like it +1 Vote: I do not like it

        In your code:

        if(q*cntprime[i] <= p*cntpal[i]){
            cout << i << endl;
            return 0;
}

        q*cntprime[i] and p*cntpal[i] can be >= 2^32 but you used type int it makes overflow.

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      I guess the doubt of sunkuet02 originates from the fact that there is no strong mathematical proof with the upper bound in this logic. Although we, the competitive programmers often think like 'Accepted = Correct Logic'. Honestly, I also set the upper bound as 2 * 106 with vague guess(with the prime number theorem), hoping that there won't be any countercases.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Strong mathematical proof was used to proof the 107 bound.

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +14 Vote: I do not like it

        See, the actual proof gives the bound of 107. You can actually run the program with 107 on your computer during the contest to make the bound to be 2·106 which is much better.

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I really don't inderstand why n<10^7

      Can anyone explain it rigorously ??

      → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't understand logic of editorial too, but I understood for n>40 pi(n)/rub(n) > pi(n-1)/rub(n-1). Then with brute-force found for A = 42 answer is 1179858.

    → Reply
»
9 years ago, # |
← Rev. 4   Vote: I like it +57 Vote: I do not like it

Using randomization in D is really unreasonable. Assume n is high and take just first 26 lines. We can check all O(26^2) intersections and if there is no such one that it has at least 6 lines passing through it we can answer NO, and if there is one, we need to take it and proceed recursively.

After that phase we can assume that n<=25 and k<=5, what we need to do here is a creative bruteforce, I used an observation that we need to take at least one point which has at least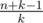 lines passing through it. Another important observation is that if we consider two sets of lines passing through common point then they have at most 1 lince in common, so there can't be many points having many lines passing through it (if n=25 there won't be more than ~7 of them), so that's the point where I used my common sense which told me that branching over "big" points will be sufficient.

Btw, what I'm pretty proud of is that I managed to use one code for both parts (http://mirror.codeforces.com/contest/568/submission/12452255) :P

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    It's great, thank you for your solution!

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    FWIW, what you did in the first phase is called kernelization :) Too bad I didn't read the problem, it's quite nice.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Wow, great solution!

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I have a question about your solution. Somewhere there, when you've just found a point which is on at least min_sz lines(of course min_sz from the first, on your example, 26 lines, in general from the first K ^ 2 + 1 lines) you have 2 cases. In the case when you have N > K ^ 2 you directly return the recursive result, but there may be some other ways to get a solution(if this way returns 0, than everything will be 0, but you didn't even try some other way to choose a point which is on at least K + 1 lines). So my question is, in case of N > K ^ 2, why do you stop the recursivity at the first point which meets the condition?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      If I have n > k^2 then min_sz = k + 1 and if this point won't be taken into solution then since those k+1 lines don't have anything in common but this point I will need to use at least k+1 points to cover those lines, which is too much. Because of that I'm 100% sure that if solution exists then it has to contain that point, so I can directly return result of recursive call here.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Thanks a lot. I understood it. That's an awesome solution :)

        → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Could explain how did you compute complexity of recursive solution of Div1 D?

UPD: ok because it's O(N * C(2,2) * C(3,2) .. * C(K,2) )

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We should try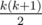 variants for fixed k. To mark used lines we spend O(n) time.

    Product of this fractions is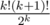

    Complexity —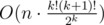

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

Can someone explain how to solve div 2 A? I didn't get it from this editorial. What is x?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 5   Vote: I like it +6 Vote: I do not like it

    x is downloaded seconds of music when we must replay music again.

    speed of downloding music seconds = q-1

    speed of listening to music = q reachtime = the time that will spend from the moment that we play music for the first time until we reach download limit.

    This "reachtime" for both actions "downloading" and "listening" must be equal. So we will calculate "reachtime" for both actoins.

    reachtime for listening = x/q (why? because: (downloaded amount)/(speed) is equal to time (eg. distance/speed=time)).

    reachtime for downloading = (x-s)/q (!when we play music for the first time we have downloaded s seconds of music and must download (x-s) seconds more)

    and now:

    reachtime for listening = reachtime for downloading

    x/q = (x-s)/(q-1)

    after solving above equation:

    x=qs

    → Reply
»
9 years ago, # |
  Vote: I like it +57 Vote: I do not like it

Another approach for 568B - Симметричное и транзитивное:

Let Bn be the number of ways that a set on n elements has an equivalence relation. It is known that a relation R is an equivalence relation on {1, 2, ..., n} if and only if it partitions the set. Therefore, Bn counts the number of ways to partition the set {1, 2, ..., n}.

Now, let Cn be the number of binary relations on {1, 2, ..., n} that are symmetric and transitive but not reflexive. The number Cn is what we are looking for. Note that for any binary relation counted by Cn, there is a set of elements that are partitioned already and a set of elements that are not in any part of the partition.

I claim that Bn + Cn = Bn + 1. This will be established by a bijection. Take any partition of {1, 2, .., n} and add the set {n + 1} to it. This will create a partition of size n + 1. Now for anything counted in Cn, take all the elements that are not in a partition yet and put them together in a set with n + 1 and this will create a partition for n + 1. This is easily seen to be a bijection.

Thus, the answer is Cn = Bn + 1 - Bn. Fortunately, Bn is a really well know sequence called Bell numbers: https://en.wikipedia.org/wiki/Bell_number. The relation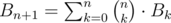 helps compute Bn in O(n2) time and O(n) memory. Then it is easy to compute Cn.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    Dang you are a cool guy

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Now for anything counted in Cn, take all the elements that are not in a partition yet and put them together in a set with n + 1

    I love the idea here :)
    Also thank you for pointing us to Bell numbers (I love combinatorics!).
    It took me a day (not in a good health condition atm, feeling stupid) to grasp all these.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it -20 Vote: I do not like it

    sorry for necroposting but I love you.

    → Reply
»
9 years ago, # |
  Vote: I like it +19 Vote: I do not like it

I think this code is really easier to understand than this big editorial for B div1.

The idea is a dp that iterates over all i < n, and put it on a existent group, ignore it or create a new group with this i. The third parameter only says if already ignore some i.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Wow, man, that's impressive :)! I have though that mine code is clever, but you definitely beat it :). Even any binomial coefficients!

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    { You code is great. I understand your code but I just don't understand what it is that the problem requires us to do. ( Sorry but the problem statement looks confusing to me :'( }

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can someone explain what this means from Div1 B, in a simpler way, or with pseudocode?:

So first part can be solved using dynamic programming: dp[elems][classes] — the numbers of ways to divide first elems elements to classes equivalence classes. When we handle next element we can send it to one of the existing equivalence classes or we can create new class.

→ Reply
»
9 years ago, # |
  Vote: I like it +23 Vote: I do not like it

One slight hole in the test data for div 1 C — solutions that just use a "topological" sort of the entire implication graph rather than of the SCC-condensed graph still pass: 12459610

Example test breaking my above solution (uses some things specific to my implementation, and almost all AC submissions during contest pass it):

CV
6 9
1 C 2 C
1 C 2 V
3 C 5 V
5 V 4 C
4 C 3 C
3 C 6 C
6 C 3 V
6 C 5 V
6 C 4 C
aaaaaa
→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Poblem div1 B. Can you explain me why in test 4 answer is 37

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

Can anyone please tell me what we have to do in problem "Symmetric and Transitive" i didn't get? please explain.. :(

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What is 2-SAT ? please explain or give some useful links...?

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Problem:DIV2 C In editorial The number of palindrome O(sqrt(n)) but when n=10 then the number of palindrome is=9 but sqrt(10)=3.16 i found mismatch .. Please explain it ..

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Don't you familiar with big-O notation?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I know it,but i could not think in that way.. thanks

      → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Div1 B. Can you please name relations when n = 3?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    1) empty

    2) (x x)

    3) (y y)

    4) (z z)

    5) (x x); (y y)

    6) (x x); (z z)

    7) (y y); (z z)

    8) (x x); (x y); (y x); (y y)

    9) (x x); (x z); (z x); (z z)

    10) (y y); (y z); (z y); (z z)

    P.S. I have a question: how to write a new line (I use Shift + Enter and get empty lines between maybe there is alternative way)?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      You can print two space after the line
      like this

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you!

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      <Br>

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Sorry, this is a bit late, but I'm not sure why set #8 is not reflexive, since it contains (x, x) and (y, y).

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        but it doesn't contain (z,z)....since n=3 for the relation to be reflexive it must contain (i,i) for all i from 1 to n

        → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Problem 569A has a shorter solution. Because sequence {xn} is geometric progression with ratio q, xn = S·qn >  = T. Thus, .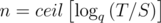

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes, that is correct formula. But computing directly the formula can get WA.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Isn't there a paradox in div2 A? For example, if it takes t time to listen to the x seconds downloaded, then when t is reached, some seconds of the song has been downloaded in that time. Then this repeats over and over again, so that you can never really reach the end of the song?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem C Div2:"Then we can calculate prefix sums (π(n) and rub(n)) and find the answer using linear search." What is Prefix sums in the statement?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Prefix sums : ith number keeps the sum of 1-i.

    → Reply
»
9 years ago, # |
  Vote: I like it +16 Vote: I do not like it

FWIW: solved Div1C without any 2SAT: 12578725 Unfortunately, not during the contest:)
Precomputed all possible implications transitively from the given ones (O(n^3), Floyd-Warshall like). Then used them to check feasibility of a fixed prefix in O(n^2). Overall complexity — O(n^3), which is the same as given in the editorial (O(nm)), but IMHO the logics is somewhat simpler.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone help me? I tried solving div1E problem and I'm getting Time Limit exceeded: http://mirror.codeforces.com/contest/568/submission/12902289 What's strange is that function Read () is getting TLE alone...I really don't understand why it is moving so slow. All it does is to read the input and sort vector B :(. Thanks in advance

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem div1D, I have a question that why the probability of the two arbitrary roads are intersects in such a point is at least 1/k

→ Reply
»
9 years ago, # |
  Vote: I like it +18 Vote: I do not like it

There is also a hole in the test data for div 1 D:

I thought this was a really nice problem when solving in practice, kudos to authors. Unfortunately my solution back then was wrong :(

Some people (me) thought that if a point goes through at least N / K points, then it must be in any good configuration. Some other people thought that any point with a maximum number of lines through it is in any good configuration. Both of these statements are false. For example, consider

N=4, K=2

test

The red point has both N / K lines and a maximum number of lines through it. However, if we use this red point, we cannot find a solution. Of course, there is a solution, demonstrated by the green points.

Mine (12458083) fails on 

4 2
1 0 2 (point 1)
-1 1 100 (point 2)
1 0 1 (point 3)
1 1 100 (point 4)

By rearranging the points (to account for randomness), 12453450 fails on 2413 and 12448661 fails on 1324.

Of course, it is rather hard to catch such bugs, since for this test we would need 6 tests, one for each choice of the first two points. Also, some people did the same thing with multiple iterations (12453811) which is probably almost impossible to break, so there is an alternate solution to be found here.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The solution of 568D is helpful for me.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem D-div 1, could anyone explain me why if a point belongs to at least k + 1 roads it must be in the solution? Thank you!

→ Reply
»
9 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

I did Div2 A by Geometric progression ( Complexity -> O ( 1 ) )

Code

We have S seconds of song available and q seconds of playback gives ( q — 1 ) seconds of download. So for S seconds we will have S * ( q — 1 ) / q more download. For S * ( q — 1 ) / q seconds we will have S * ( q — 1 ) * ( q — 1 ) / ( q * q ) more download and so on. This will go till infinity and total sum of these values will give total time music played until music stops because of incomplete download. This is geometric series where first term is S and common ratio is ( q — 1 ) / q. So sum will be S / ( 1 — ( ( q — 1 ) / q ) ) which is equal to S * q.

So for S seconds of download we can listen till S * q seconds and then we will have to restart. Now we will have S * q seconds of download for which we can listen upto S * q * q seconds. This will go until it is greater than or equal to T. So we will have something like S * q * q * q . . . * q = T. Answer is number of times q.

Number of times q = log ( T / S ) to the base q.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    wonderful solution ! and well-explained.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Maybe i'm wrong, but why logl( X ) where X is some number works in O(1).

    So I think your solution works in O(log(t) + log(q)).

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I can't understand the solution to Div 1B.

So first part can be solved using dynamic programming: dp[elems][classes] — the numbers of ways to divide first elems elements to classes equivalence classes. When we handle next element we can send it to one of the existing equivalence classes or we can create new class.

We're trying to compute the number of equivalence relations in a set of size x.
How does this transform into a "partition x numbers into g groups" dp?
What does a group/equivalence_class actually denote?
Could someone please elaborate?

→ Reply