At midnight from tuesday to wensday 00:00 GMT will be held 666th Topcoder SRM. (Tuesday evening in the Americas, Wednesday night-evening in Eastern hemisphere)
Learn Latin! :) In hell, nobody would speak to you in English! :)

| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 170 |
| 2 | Um_nik | 162 |
| 3 | maomao90 | 161 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 158 |
| 5 | -is-this-fft- | 158 |
| 7 | adamant | 154 |
| 7 | Dominater069 | 154 |
| 9 | awoo | 152 |
| 9 | luogu_official | 152 |
At midnight from tuesday to wensday 00:00 GMT will be held 666th Topcoder SRM. (Tuesday evening in the Americas, Wednesday night-evening in Eastern hemisphere)
Learn Latin! :) In hell, nobody would speak to you in English! :)

| Name |
|---|



The contest will be in morning (6:30) in India, it is going to be a tough time ahead for me to get up in the morning :P
You have just saved me before waking up at 6 AM — I am currently in USA and timeanddate.com showed me it will be on 6:00 and I thought that I will have to wake up early, but thanks to you I realized that it was 6 PM :P.
I guess scoring will be 333-666-999
I guess scoring would be usual :P
Both of you missed :)
Quite unluckily, no fourth problem scored 161616.
... and sad part is me missing this despite being round writer :(
whine Why haven't you introduced some satanic elements into story? whine
Hi beatoriche, sadly I did not know significance of satanic elements being related to 666 before somebody told me about it after the end of contest. Now I am feeling sad about it :(
TCP port 666 is reversed for DOOM game :-)
It will be 4 AM here in SYRIA, but thanks for reminding me :)
Anyway I will find a strategy to wake up at this time :D
Good luck! You can do it
8-10PM here in the U.S!
666: Can it be??
▲ `-.`'.-' `-. .-'. `-. -./\.- .-' -. /_|\ .- `-. `/____\' .-'. `-. -./.-""-.\.- ' `-. /< (()) >\ .-' - .`/__`-..-'__\' .- ,...`-./___|____|___\.-'.,. ,-' ,` . . ', `-, ,-' ________________ `-Commenting here so that this blog comes back into recent actions.
Hell has opened its gates, I mean, registration has started.
Ugh, I haven't seen more repulsive problem than 888 in a long while >_>. TankEngineer submitted it in my room, so after realizing how tedious it is in coding phase I decided to prepare a test which will cover many stupid cases and challenge him blindly with it and it turned out to be a good choice :P. Currently there are still 4 unhacked submissions, but I will be surprised if at least one will be correct...
What was the test case? Turns out that you're really lucky — all other submissions for 888 are correct.
Hah, yeah, indeed it looks like I was very lucky on this one : D.
This was the test:
Is there an option to somehow execute other people's solutions? I would like to test them against this testcase :P. However afair tests from successful challenges are added to systests, so it is very improbable that those accepted solutions will fail at this one, right?
Btw in statement there wasn't mentioned is that possible to have identical intervals and my test contained such on beginning but it was rejected because of that :d.
It was mentioned in the 'constraints' section that no two intervals are equal.
What is so special about your testcase? What is the correct answer?
OK, so maybe I overlooked that equal intervals, nevermind :P.
If you look from a correct angle on this problem then maybe there are no special testcases at all, if you would be looking from angle I have used (not the best one) then you would observe tons of ugly cases :P. Since I didn't complete coding I don't know what is the answer — I was informed what is the correct answer when hacking, but I didn't write that down.
I dunno, it didn't seem all that ugly to me. A lot of cases can be cleared by adding leaves representing spaces not in the given intervals and one topmost interval (the condition of even sum is just a matter of one zeroing loop). Then there's just the case of filling a small interval with all 1s.
I could've done it (maybe) if I hadn't moved to 222 thinking I'd solve it quickly and return...
Just to be sure that we are talking about the same solution — I assume that intended solution is something like dp[interval][number of ones from left][number of ones from right] in tree formed by intervals with additional beautiful case of whole interval covered with ones? It looks like it could definitely be done like that, however number of weird things to check is over nine thousand. After fixing those number of ones from left and right they can arrange with children in many incredibly annoying configurations, not to mention that case with all ones...
I have to admit that I'm really surprised that someone managed to get this accepted, so maybe I'm just missing a nice way to cover many cases in some tricky way or I'm looking at whole problem from a misleading angle.
That's the one, but with [parity of the sum] to the DP states. The case of "whole interval covered with 1s" is just when length of the interval = number of 1s from the left = .. from the right and suitable parity, and there are just one or two special ifs for that when merging.
Ahhhh... so thanks to adding those new intervals we can proceed with always merging two adjacent intervals! Really clever!
Could you provide some more details of you solution. I could not understand the 'dp[interval][number of ones from left][number of ones from right]' part. How do you build the answer for an an interval?
Really not much point in that since even I didn't work out the details, I started coding at moment when I thought "that can be done". Better please refer to one of accepted codes, for example zxqfl's one http://community.topcoder.com/stat?c=problem_solution&rm=326874&rd=16515&pm=13767&cr=23072570 Main logic in function SolveInterval looks at least 10x shorter than what my solution would look like :P.
Whoa, that's fast system testing.
yeah :D there should be more contest like this one
There shouldn't be. Fast systest = few submits.
TopCoder => few people
Hour terrible for Europe => few people
few people => few submits
Topcoder => few problems
few problems => few submits
However I think that easy and med were really easy in comparison to what we have experienced recently.
I was the only one who couldn't challenge others?
In Div2 Problem C I realized it was DP, but how to approach it?
222 is almost same as this one
Well, it's pretty hard to come up with problems that don't appear anywhere, especially on the easy slot.
I also helped prepare almost the same problem here (in Portuguese): http://br.spoj.com/problems/SAOJOAO/, I guess this certainly helped me to get fastest time on it on TC :P
I really shouldn't procrastinate to solve this br.spoj is problem :(
Well, now that everyone has mentioned the solution it`s almost trivial. you just have to do it once for each query. :)
Yeah I have also seen the problem 222 before — in fact for much larger tree and path sizes.
I literally facepalmed when I realized how to solve 222 Div 1. It was surprisingly easy! And It took me an hour to realize the simplicity of it.
Can you please explain your solution.
Find maximum depth using bfs/dfs, let it be d
if (L<=d) ans=L+1; else ans=min((L-d)/2 + 1 + d),n);
Could you explain ans=min((L-d)/2+1+d,n) part?
Consider the path from the root to the farthest leaf (depth of which is d). Travelling along this path from root to that leaf takes d steps (assuming root is at depth 0). Now you have visited d+1 nodes and have L-d more steps available. Now, for all other vertices not on this path, to visit them, you will take 2 more steps per vertex, no matter where they are. So, using L-d steps, you can visit at most (L-d)/2 more vertices. So total vertices visited is d+1+(L-d)/2. But this value may exceed n if L is very large as compared to n (eg. n = 3, L = 100). So the answer will be minimum of this value and n.
How to solve Div 2 Hard using DP?
For solving Div 2 Hard, first you need a main observation from Div 1 easy. After that, you can use some knapsack sort of dp.
I didn't take part in the contest, but I found 444 much easier than 222.
I did them on practice mode and got 300 points on 444, but only 78 pts. on 222. The middle problem is very straightforward (divide the array into 2 or 3 parts, multiply accordingly, do combinatorics, etc.), while the "easy" problem requires a lot of case handling (Do I have to return here or do I finish elsewhere?, how many extra moves do I need to return to this node? (2?, maybe 3?), how many moves do I spend on this child and how many on this other one?, etc., etc.). I spent over half an hour debugging it...
http://community.topcoder.com/stat?c=problem_solution&rm=326872&rd=16515&pm=13955&cr=22926197
Yeah I had a similar solution but if one doesn't know that then it's not exactly clear to me what one does. Presumably you can do some sort of a dp where f(Node,path_length,am_i_returning) tells you the greatest number of nodes you can visit from a particular Node in the tree going downwards with path length and returning to the Node depending on am_i_returning. But this does seem quite ugly.
That's precisely what I did, and it also needs an inner DP on the children to know which of them you must visit and which to skip.
I would have never thought of that. That's really very smart.
I did DP[v][m][f], which is the maximum number of nodes I can visit starting on node v with m moves left, and f indicates whether I have to return to this node or not. Then, inside the DP, another DP ch[i][j] on the children meaning how many nodes I can visit if I use up to "j" moves on the children and I already processed i of them. Then, finally if f = = 0, we need to skip one child in that inner DP because we will finish our travel inside that child's subtree. You can imagine the time I spent coding and debugging all of that... what a useless waste of time considering how simple the intelligence solution actually was.
Can somebody explain the method to solve Div 1. 444 problem?
The trick is to consider the last number in the permutation. Let DP[k] be the answer for size k. Then we have 2 possibilities: The last element is at the border (left or right) or it's in the middle. If it's in the border, it multiplies by n - 1, otherwise, it multiplies by n - 2. So, initially we have the value 2 * (n - 1) * DP[k - 1] for the cases when the last element is at a border. Then, consider we choose last element m, which is not in a border, then we will have a left portion of size l and a right portion of size r. Those two portions won't be connected, which means they are independent. We have every possible combination on one side multiplied by every possible combination on the other side. That means (n - 2) * DP[l] * DP[r]. But we're not quite finished yet, because we can alternate between choosing elements from one side and the other. The total number of ways to alternate between choosing elements from a section of size l and a section of size r is C[l + r][r] (combinatorics). So, for every m in the middle, we must add (n - 2) * DP[l] * DP[r] * C[l + r][r], where l and r are the remaining elements at each side of m.
I hope I was clear, it's not easy to explain with words...
You have to compute DP[1.. n][0 .. 2], where second dimension is number of taken borders, you completely disregarded number of taken borders in your description :d.
I mentioned the borders part at the beginning. The recurrence for the DP function would be...
Ahhh, sry, you're right. I considered first element, not last one and that mislead me, your solution is better :)
i could not clearly get the combinatorics part :( can you please explain ?
Suppose you have a collection of red and blue balls, R red balls and B blue balls. There is no way to distinguish between two different balls of the same color. Your task is to put all R+B balls into one big box. How many ways are there to put all the balls into the box if you can take them in any order? Two ways are considered different if at some step, the color of the ball put into the box in that step is different.
The solution: Consider an arbitrary arrangement of length R+B "RBBBRRBRBRB...R" corresponding to a given configuration. The question is analogue to "How many such arrangements are there?". You know the total length of the arrangement is R+B and exactly R elements are "R", so the answer is simply combinatorics for R taken out of R+B =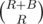 .
.