→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 21:39:05 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











After long time finally I received notification mail from TopCoder about SRM 667 :D
Can you compete there without using their's Arena? I cannot connect with it to the server...
Had you tried http tunnels instead of direct connection?
The button 'Autodetect' doesn't find anything.
Try clicking on Direct and selecting either tunnel A or tunnel B. Sometimes even Direct (China) is working
Just went through all the options... none of them work.
Run the applet using the console (under Linux, for example, this can be done by using command "javaws ContestAppletProd.jnlp" where ContestAppletProd.jnlp is a jnlp file of Arena), then there will be some debug information in the console output.
When I wasn't able to connect in similar strange way last time, I found out errors of form "Proxy server doesn't listen to incoming connections". The reason for me was that Arena tried to take network options from Firefox (that is not even a default browser in my system), and there was an option of SOCKS-proxy being set for some reason. After I disabled it, everything worked fine.
Make sure that there are no system-wide or default browser network options (like proxy server being set up or anything else) that prevent Arena from connecting to the server. Also try to read console output, maybe you will find out what's wrong there.
I've installed jdk and tried to run it with appletviewer and with javaws. appletviewer does nothing and javaws simply starts the arena without any debug output. Then I decided to monitor the activity with procmon, but I failed to discern anything meaningful in that output. Wireshark did't show me anything useful neither. Now my toolset is exhausted.
Then I had a quick thought that maybe I should try installing linux on virtual box, but then I realized that it would be an overkill and I ain't that desperate — I can wait for another codeforces round ;)
What are the plug-ins that can be used inside the arena to get ready-template for writing the code directly without writing the class and other needed things for Top-coder contests?
KawigiEdit
I recommend Greed 2.0 plug-ins.
All greedy solution failed or even DP solution failed for D2-500 or D1-250. People in Div1 got 500+ only through challenge wow.
No mine passed :D
Did you have a greedy solution?
No, it's dynamic programming solution, check this: LINK
How did people obtain these magical formulas in 500? I was trying to solve it for the whole contest, and the best I could get was some recurrent magic which had precision issues. Am I missing smth obvious?
I started solving this problem with implementing brute force :)
After printing its results things are more or less clear — but I am also curious how to come up with these formulas in some analytical way.
Could you explain how you wrote a brute force for it ?
I used most naive one — let's calculate probability of having mask of covered people Mask and current person P after N steps; here is the code: link. If needed — you can improve it by storing left and right borders of covered interval instead of a mask (it is quite obvious that covered people are represented by contiguous interval); however, for me such solution sounded more complicated and I was not sure that I'll write it without bugs in a short time.
Oh I see. Thank you. Btw the link doesn't work but your explanation is clear enough.
Lets solve original problem for a sequence (not for a circle), by cutting before K and after K.
So, we can reformulate the statement as following: probability of handing the ball from ith cat to 0th cat and we can't go beyond 0th and (N-1)th cat.
Let's calculate dp(i);
dp(0) = 1
dp(i)=dp(i-1)*p+dp(i+1) *(1-p), (0 < i < n-1)
dp(n-1) = dp(n-2) * p
dp(n-2) = dp(n-1)*(1-p) + dp(n-3)*p;
it means,
dp(n-2) = dp(n-2)*p*(1-p)+dp(n-3)*p, so we can simplify it to:
dp(n-2) = p/(1-p*(1-p))*dp(n-3)
Shortly, dp(i)=coef(i)*dp(i-1), where coef(i) is found using algorithm above.
I think this algorithm with some cut-off for N (something like N=min(N,1e6)) can pass System Test.
I couldn't find bug in my implementation during the contest, so I don't know will this with cut-off pass or not.
Wow the last couple of lines for dp(n-2) were quite nice thank you.
Did you get it accepted?
If we have a segment [0..L] and want to find out the probability P(x) of getting to L from x without stepping out to - 1 (1 minus the answer to our problem can be reduced to 2x that), and the probabilities of moving right/left are p and 1 - p, then we have pretty obvious recurrences:
If we write $P(x)=P(0) k_x$, then k0 = 1, the first one gives k1 = 1 / p and the last one
If we expand the right side as kx + 1 - kx + kx - kx - 1 and denote kx + 1 - kx = dx, then we get dx + 1 = qdx, where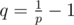 . From this, it's easy to see that dx = qxd0 and since d0 = q once again,
. From this, it's easy to see that dx = qxd0 and since d0 = q once again,
(of course, funny stuff happens when $p=0.5$, but then dx = 1, kx = 1 + x and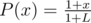 ). This formula holds for x = L as well, so we can find P(0) = 1 / kL and
). This formula holds for x = L as well, so we can find P(0) = 1 / kL and
We can see that this seems to work for corner cases of $x=0,1,L$. Badum-tss!
Could you kindly explain this? I don't understand how to make this reduction...
If cat K loses, then it gets the ball through one of its neighbours, while the other neighbour didn't get the ball yet. So cat K is that L and the other neighbour is that - 1. There are 2 choices of which neighbour and we need to consider both.
I will try to explain what I don't understand.
We walk on [0, ..., L]. If we start walking at position k, to win the game we have to visit all positions, but L, first, and then we can enter position L. Then initial problem is equivalent to finding probabilities of finishing at L and starting from positions K and N - K. Correct me, if I am wrong.
So, to conclude. If we consider problem on range [0, ..., L], before getting to L we must visit all position on sub-range [0, ..., K - 1]
Do you have code for your approach?
p.s. Can you kindly fix issue with formulas in your comment above?
UPD: I think here is what I wanted to know. Thanks anyway for all your comments above.
I'm talking about what to do to lose the game ("if cat K loses"). Think about that first.
alright, got it! thanks!!
Gambler's ruin is a rather known problem.
+100, I've written a reccurrence in 15 minutes, then thought that the stupid solution will help to deal with cases when n is small. After that I implemented an O(n^2) DP and noticed that the probability distribution forms a geometric progression.
It would be very cool if there is a nice mathematical explanation for that fact.
could you describe your O(n^2) approach? I have been trying same, but did not observe any recurrence... I might had a mistake :(
Calculate DP[l][r][w = 0/1] = probability of situation when there are l visited points to the left of 0, r to the right of 0 and we are standing in - l if w = 0 or in r if w = 1. From DP[l][r][w] we may move to DP[l + 1][r][0] or to DP[l][r + 1][1] with certain probabilities that may be found using some simple probabilistic equations (by reading comments in this topic I found out that this is called Gambler's ruin, wow :) ). The answer can be found as sum of DP[n — k — 1][k][1] + DP[n — k][k — 1][0].
I have been thinking about this DP, have tried exactly same DP state, however did not manage to understand what the formulas are. I did not understand how to describe the fact that before going out of the considered range we can walk as long as we want inside range. Could you kindly clarify the logic? Or if it is possible share your code?
The task is equivalent to the following. We have points 0, 1, ..., n and a person staying in point k. In each step person moves right one position with probability p and left one position with probability 1 - p. When he reaches 0 or n it finishes its walk. What's the probability to end up in position n?
Let's denote probability to end up in n starting from k as Ak. Then we have formulas: An = 1, A0 = 0, Ak = pAk + 1 + (1 - p)Ak - 1. Let's rewrite last formula as (1 - p)(Ak - Ak - 1) = p(Ak + 1 - Ak). Denote Ak - Ak - 1 = Δk. We have (1 - p)Δk = pΔk + 1, so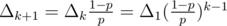 .
.
On the other hand, Δ1 + Δ2 + ... + Δn = An - A0 = 1. So, . From this we can find Δ1 and all other Δk, and Ak as Δ1 + ... + Δn.
. From this we can find Δ1 and all other Δk, and Ak as Δ1 + ... + Δn.
Here is a fairly well-known argument.
Denote the probability of player i to be the last as Pi. Consider what happens with player k for k in {2, ..., n - 2} right after player 0 passes the token for the first time (and only once!). The player k will find herself in the state that player k - 1 was in before the game started with probability p and in the state that player k + 1 was in with probability 1 - p, so
Pk = pPk - 1 + (1 - p)Pk + 1, or
In the case of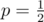 this immediately gives the result once you observe that p1 = pn - 1 by symmetry. But you have to go a little further to get to a solution from here and direct application of Gambler's Ruin is probably easier.
this immediately gives the result once you observe that p1 = pn - 1 by symmetry. But you have to go a little further to get to a solution from here and direct application of Gambler's Ruin is probably easier.
Welcome in my club, one hour was also not sufficient for me, not a good day for me >_>.
All you have to know is https://en.wikipedia.org/wiki/Gambler%27s_ruin
Firstly we count probs for cats 1 and n-1 using gambler's ruin. Then for a particular k we count probs that k-1 will have ball earlier than k+1 — this is also gambler's ruin. If k-1 has ball earlier than k+1 then prob for k being winner is prob for 1 being winner in an original game.
I didn't get a simple formula as most, but I started by the already-known result of the Gambler's ruin: https://en.wikipedia.org/wiki/Gambler's_ruin
Let GR(a, b, p) be the probability that in a linear walk between 0 and b, starting in a and having probability p of going right and 1-p of going left at each step, you hit b before you hit 0.
Knowing this, the probability that K will be the last is:
The probability for each of case 1 or case 2 happening is another application of the GR formula (case 1 happens with probability GR(N-1-K, N-2, p)).
No, the problem is anything but obvious but it reduces to a well-known one. In fact the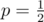 case was once given at the Olympiad in Probability Theory in MSU. I've written the solution to this case below.
case was once given at the Olympiad in Probability Theory in MSU. I've written the solution to this case below.
Upd.: It turned out to be above -- not below -- because of the nesting rules!
I can't tell properly why but I completely dislike problems like div1-500 on short rounds. When the solution is a short formula and how you deal with task transforms into half-hour maths investigation or "writing a brute solution and looking for pattern", I think, that's not a task for a programming contest but more like ProjectEuler or math contest task.
I think they are really fine and such problems with short solutions are kinda in TopCoder style. Idea is also really simple, if you have right idea then whole "math investigation" is really not that complicated and to create a brute-force you still need to have an idea how to write brute-force and I don't know such solution yet even though I know solution with direct formulas. And I think that I will fail in observing pattern, such solutions are really risky. Firstly you need an idea for bruteforce and waste time to write it and in most cases formula will be too complicated to observe simple pattern.
Knowing when to move to a different problem is an important skill.
The fact that task is "maths/pattern investigation" doesn't always correlate with "it's better to move to a different problem". Sometimes such task is pretty easy and you have to perform investigation steps because there will be 100 people who will do that and otherwise you'll end up in the bottom of the ranking table.
That doesn't mean I dislike such tasks at all, but I think they are not proper in the situation when the round is very short. In ICPC-like contest it's much more convenient to sit with a piece of paper or with printed first values of a sequence and to think on problem while your team-mates are coding something.
"but I think they are not proper in the situation when the round is very short." — I beg to differ. I think round being short is exactly what makes them proper. Since code is short, not much place for a bug, whole problem can be solved in 10 mins of you have right idea, main difficulty focuses on coming up with solution, not on coding which usually takes majority of time. I pretty much dislike topcoder problems when there is a lot to code, how am I supposed to write bugfree code consisting of 100 lines when I probably have ~20 mins for that?
This problem can be solved without "writing a brute solution and looking for pattern" / do "maths investigation".
So what you want to solve is like:
(*) tells us how to get x[i] from x[i-1] and x[i+1], that is not useful, so we rewrite it into x[i+1] = a * x[i] + b * x[i-1] (calculating a and b is the only thing you need to do by hand).
Then you just set x[1] = 1, and use this new equation to get x[n+1] by fast matrix multiplication, say, we get 100. Then that means x[1] should be 1/100 instead. And after that we can get x[k] by using fast matrix multiplication again. I think this idea itself is algorithmic.
You can see my code here: http://ideone.com/Eeropa
I tried to do exactly the same thing, but had problems with huge numbers on large test cases. The idea itself is algorithmic (although instead of inventing a bicycle one could look up the formula in Wikipedia), but there are lots of caveats with precision, large numbers, etc.
Could you explain this part of your code as well?
Can anyone share the approach for DIV II — 500 ?
I think you have to keep the remaining number of strings that doesn't processed yet and also the mask for the processed ones, (It's enough to keep the mask but it's simpler to keep the remaining number also).
so the dynamic state is
(rem, mask)so all you have to do is to have the mask that you have already handled (if the column
jhandled before) so let's call itmask1, so this can be calculated by O(n) if you have already processed the masks that any string may use first.so loop on all possible strings (
nstring) if it's not processed before (you can know that from the dynamic mask) process it and count not processed columns inside it, the processed ones found insidemask1, so now the problem is simple!Congratulation to KADR! Winning contest by solving first problem. What a challenge monster! Was this achievement reached before?
Thanks!
Welcome to the parallel universe, where people win rounds by only solving easy and this happens:
EDIT: Sorry bmerry, forgot to include you at 210th place. Anti-target round indeed...
Congrats to subscriber on becoming a target finally!!! I'm enjoying your videos!! Waiting for this one ;)
p.s. I hope you won't stop posting your videos.
Can anyone explain how div-2 500 can be solved ??
One-word hint : Knapsack!
can you explain a bit more?
dp[mask] -> minimum cost for reaching the state where '1' bits of mask represent cached memory positions. Therefore dp[s[0] | s[1] | s[2] | ... | s[n-1]] is the answer. Can you come up with the transitions ?
using first k strings? is it dp[k][mask]? otherwise, if its plain dp[mask], it seems hard
I think dp[k][mask] will do the job too but you'll notice that dp[k][...] will only depend on dp[k-1][...] and therefore dp[2][mask] is enough. And also index i (i is a mask) will only affect some index j where j > i, and this means you won't need all of the values of dp[k-1][...] for dp[k][...] and can update the values on the fly, which means dp[mask], with the transitions exactly like those of knapsack (but with min instead of max) will solve the problem. Let me know if further explanation were needed.
Wow, I submitted 250 for 99 points and thought I did badly without looking at the rankings, and it turns out I was the only one in my room to get a single AC...
Did any explained DIV1 250 ??
I saw that most of solutions uses DP with bit mask state, but I couldn't understand them.
Can someone please explain how did you came up with the DP state.
1 — preprocess all the strings and get the mask of every string, the mask is the (1s) inside the string, and save the mask for string
iascost[i].2 — Do Dynamic programming as follow:
The state
(int rem, int mask), rem: the number of strings not processed, mask: contains the strings that processed, you can loop on all the strings, if it's not processed try to process it like this:F(rem, mask) = F(rem-1, mask | (1<<i))for every string not processedThe cost is the number of (1s) inside the string
ithat not processed yet, how we can do it efficient, think about, you can usecostarray.