A. Mirror-number.
First note that if the interval contains a number with a digits and a number with b digits (where a > b) then there is no need to consider the number with b digits (as the weight of 10^k is greater then the weights of the numbers less than 10^k).
If we consider only numbers with fixed number of digits (s + 1), then the sum of a and its reflection is constant. Thus, as product grows as multipliers with fixed sum get closer, the picture is the following: the weight grows from 10^s to 5· 10^s - 1, then it stays the same for 5· 10^s and then it goes down, and reaches its minimum (zero) value at 10^s + 1 - 1.
This is the proof, and the solution is: the maximum weight is reached at either l, r or 5· 10^s (we may check all the s such that 5· 10^s belongs to the interval, for example). 

B. Tetris revisited

It's easy to see that the field may be filled with such figures if and only if there is no isolated cell.

There are many different ways to do that, we will show some of them.

1. Domino filling.

We construct greedy matching on the cells of our field combining them in domino-like figures (rectangles 1  ×  2).

Passing through the array that represents our field (from left to right, from top to bottom) we combine the still free horizontal pairs of connected cells into the horizontal dominoes. Then we do the same thing with the still free vertical pairs. Naturally, some cells may be still free. But such cells should be adjoined with some of the dominoes (if they were not isolated). We may attach each of these cells to any of the adjoint dominoes. All resulting figures will contain no more than 5 cells, because the cells still empty after matching can not be neighbour cells and can not be adjacent to the left side of dominoes (by the virtue of the order of our matching).

The last thing that has to be done is the coloring of the figures in accordance with the output format. For example, we may color them like that: color all the cells in the plane in 9 colors  (i, j) -> (i % 3) * 3 + j % 3. Then paint each domino in the color of its black cell (according to chess coloring). Each figure will have the color of the domino it grows from.

2. Greedy.

We pass through the array representing the field, again in the same order. Figure for any still free cell may be constructed greedily, but we have to be accurate in order to avoid appearance of new isolated cells. So we just add all the cells that do become isolated when we fill the current figure. Acting in such a fashion we will eventually get the covering by the figures of no more than 5 cells (and at least two, of course).

It is possible to color the figure immediately after its formation. We only need to check the colors of all already colored adjacent figures and to take any color, different from all of them. It is not hard to see that 10 colors are enough.

C. Genetic engineering.

Suppose we've built a string wp of length k < n and want to know how many ways there exist to complement wp to the suitable string of length n.
What parameters do we need to know in order to build it further?
First of all, we need to know the index wp is covered up to (we denote it by ci and call it covering index). Also we want to have some information about what the string ends with.
Here comes rather standard idea: let's find all the prefixes ALL_P of the {s_i} and add to our state the largest prefix 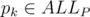such that wp ends with p_k (as an alternative, you may consider a vertex in a trie constructed with the collection's strings).
Now I'll try to convince you that it's enough to set the things going. First of all, when we add a symbol c to wp we can easily get p_k + 1 and it will be equal to the largest string in ALL_P such that the string p_k + c ends with (we can precalculate all the transitions in advance). So the only thing we want to know how to calculate (in order to use dynamic programming approach) is the new covering index. But we notice that it can be changed only by some string from the collection that w_p + c ends with. Now we observe that it is sufficient to check only the largest from all such strings (denote it fs), and that it necessarily contains in p_k + 1 (so it also can we easily precalculated for all strings in ALL_P). We observe further that the new covering index depends only on the length of fs: it either equals the old one if fs doesn't cover the symbol ci + 1, or equals to (k + 1) if the fs covers that symbol.

After calculating all the quantities d[k][k - cov.index][max. prefix] the required number of strings equals the sum of d[n][0][mp] for all mp.

D. Powerful array.
Let's solve the problem offline in O(n sqrt(t)) time and O(n) memory. For the simplicity of the reasoning let t = n.

Assume we know the answer to the problem for some interval and want to find it to another one. Let us move the left end of the first one towards the left end of the second, similarly dealing with the right ends. By moving the end by one and for every value in the array maintaining the number of its appearances in the current interval, we will be able to calculate the answer and maintain the numbers of appearances at the same time in O(1). From now on we call the procedure of movement by 1 a step.

Going through the queries in such a fashion, evidently, will cost us O(n^2) steps.
Let p = sqrt(n). Divide the array into p equal parts Q_1, ..., Q_p. Now consider the queries of the form (Q_i, Q_j) for all i and j (there will be approx. n such queries). Clearly, there doesn't exist an order in which we can go through the queries in o(n sqrt(n)) time as the transition from any interval to the other one is done in no less than sqrt(n) steps.

Nevertheless, there exists a traversal order that guarantees O(n sqrt(n)) steps in the worst case.
Let's sort the query intervals according to the following rule: first come the intervals with the left ends in Q_1, then the intervals with the left ends in Q_2, and so on. And if the left ends of the two queries belong to the same part, then the interval with the more left right end is assumed to be smaller.

In order to prove the stated asymptotic behavior we will follow the steps of the left and the right ends independently. We note that the left ends that belong to the same Q_i make <= n / p steps, and transition to Q_{i+1} costs no more than 2 * n / p steps. Therefore the left ends make <= n/p * n + 2*n steps (the second summand is O(n), and it's negligible).
The right ends in the common group move only to the right, and this proves <= n * p steps (during the whole process) estimate. We will estimate the transition to the next Q_i at no more than n steps, so overall we get <= 2 * n * p steps.
Thus, the total number of steps is no more than (n / p * n + 2 * n * p). Now we choose p = sqrt(n) which proves the statement.

Solution: let us sort the queries by this rule, then make transitions from a query to the next one according to the obtained order.

Note 1. There is nothing special (except for nonadditivity) with the function in the statement.

Note 2. In the case of distinct n and t we can similarly prove the nice estimate 2 * n * sqrt(t), mostly nice because of its exactness (if you follow the proof carefully, you will easily construct the maximal test).

E. Long sequence.
Firstly let's note that there are only 49 different possible inputs.
So any solution that works finite time at all tests (even if does not pass timelimit) is enough, because we can memorize all the answers. It is not necessary, of course, but may help with slow solutions.

Then, let's answer a more particular question. Assume that c₁, c₂, ..., c_k and a₀, a₁, ..., a_k - 1 are already given and we need to check whether the sequence {a_i} generated by them is long or not. We know that if it is periodic, then it is possible to find any non-zero k-tuple among k-tuples a_s, a_s + 1, ..., a_{s + k - 1}. So initial k-tuple has no real matter if only it is not zero. Thus the property of sequence "to be long" depends only on coefficients c_i, and we may choose any convenient a₀, a₁, ..., a_k - 1. We will now think that a₀, a₁, ..., a_k - 2 are zeros and a_k - 1 = 1.

Consider the transition matrix A of our sequence: for i < k the i-th row of A is equal to (0, 0, ... 0, 1, 0, ..., 0) with 1 at (i + 1)-th position and last row of A is equal to (c_k, c_k - 1, ..., c₂, c₁).

Denote by x_s vector (a_s, a_s + 1, ..., a_{s + k - 1})^T.
Then for any integer s we have: A· x_s = x_s + 1.
Last is just a reformulation of the recurrent formula:

a_n = c₁ * a_n - 1 + c₂ * a_n - 2 + ... + c_k * a_n - k.

Then by obvious induction we have: A^p· x_s = x_s + p for any p ≥ 0. Hence p is a period iff for any vector x that appears in our sequence: A^p· x = x. If the sequence is not long then it is not self-evident still that A^p is an identity matrix, because x does not take all possible values. But we have chosen x₀ = (0, 0, ..., 0, 1) before, so it is obvious that vectors x₀, x₁, x₂, ..., x_k - 1 form a basis. Hence if A^p· x_i = x_i for any i then A^p is the identity matrix.

So we just need to do the following:

1) Construct the matrix A from the coefficients c_i.

2) Check that A^2k - 1 is the identity matrix. (If not, then 2^k - 1 is not a period.)
If 2^k - 1 is a period, then we have to check that it is minimal. Minimal period divides any period so we only need to check the divisors of 2^k - 1.

3) Generate all maximal divisors of 2^k - 1 and check that they are not periods (using A again).

(By maximal divisor of n we mean divisors of the type n/q where q is a prime number.)

Last thing we need to notice that such a sequence always exists. Moreover, amount of appropriate sets of c_i is pretty large. One may prove that there are such sets (because they correspond to the coefficients of the irreducible factors of the cyclotomic polynomial over 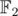). So we can just take them at random and check.