Hello, friends!
Winter 188th Codeforces Round is coming!
We wished to prepare for you some enjoyable problems (as we believe, not very difficult) with nice ideas and clear statements.
"We" includes authors of the problems yaro and Rei, Codeforces Rounds supervisor Gerald and the platform founder MikeMirzayanov. Special thanks to Pasha (PavelKunyavskiy) and Artem (RAD) for the testing and helpful comments.
Last time I was preparing a competition here on Codeforces, Rounds were still "beta". Well, with less "beta" comes greater responsibility. So I wish the authors and the organizers a successfully held Round. As for the participants, I wish you the unconventional ideas, the clean code (and a clean keyboard, of course), and satisfaction from five (well, possibly the less number will also do...) correct and accepted solutions!
It seems to us that it is not an easy job to arrange the problems by their difficulty, so we have chosen the dynamic scores. Still (out of curiousity) let us put a bet on the following relative difficulties for the problems: div.1 — B-B-C-C-E, div.2 — A-B-C-C-E. How close is our guess?
UPD Sorry for the problems with the Codeforces testing queue during the round.
We will still be happy if you rate our contest (when it will be over): short survey.
And with the gap of one hack the winner of div.1 is meret (Jakub Pachocki)!









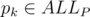 such that
such that 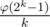 such sets (because they correspond to the coefficients of the irreducible factors of the cyclotomic polynomial over
such sets (because they correspond to the coefficients of the irreducible factors of the cyclotomic polynomial over 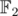 ). So we can just take them at random and check.
). So we can just take them at random and check.
