Задача A.
Все что нужно было сделать в этой задаче — разобрать несколько случаев. В силу того, что все числа были до 108 вычисления проводить можно было в 32-битном типе данных.
Разобрать нужно было следующие случаи:
Дом
первый магазин второй магазин домДом
первый магазин второй магазин первый магазин домДом
второй магазин дом первый магазин домДом
второй магазин первый магазин второй магазин дом
Асимптотика: O(1)
Задача B.
В этой задаче нужно было лишь внимательно прочитать условие и аккуратно реализовать то, что написано в условии. Изначально нужно завести для каждого элемента от 1 ... N список чисел, из которых можно его получить.
Затем нужно пройти по массиву и разобрать несколько случаев, предварительно нужно завести флажок для ответа Ambiguity:
Пусть текущий элемент массива — bi
- Если существует более одного элемента, из которого можно получить bi, то нужно поднять флажок, который отвечает за Ambiguity
- Если не существует ни одного элемента, из которого можно получить bi, то нужно вывести Impossible
- Если элемент один, то просто заменяем bi на число, из которого мы могли получить данное bi
В конце, если флажок поднят, то нужно вывести Ambiguity, иначе Possible и полученный ответ.
Асимптотика: O(N)
Задача C.
Первым делом нужно понять, как выглядит оптимальный ответ.
Пусть Hi — отсортированная последовательность hi. Пусть E — множество индексов последних элементов каждого блока. Тогда утверждается, что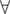 
e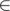 
E, отсортировав первые e элементов последовательности hi получатся в точности e первых элементов последовательности Hj.
Тогда, нетрудно заметить, что размер E будет являться ответом на задачу.
Для начала нужно посчитать два массива: prefmax и suffmin, где prefmaxi — максимум из элементов a1, a2, ..., ai, а suffmini — минимум из элементов ai, ai + 1, ..., an.
Чтобы получить ответ, нужно посчитать количество индексов i таких, что prefmaxi ≤ suffmini + 1.
Асимптотика: O(N)
Задача D.
Будем решать задачу для n ≤ m, затем просто поменяем местами и выведем ответ. Нужно не учесть квадраты два раза!
Давайте воспользуемся следующей формулой для фиксированных n и m (n ≤ m) и чтобы вычислить x.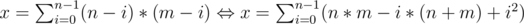 
Если еще немного упростить, то получим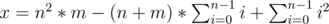 
Затем применяем сумму квадратов и сумму первых k чисел для решения этой задачи.
Получаем 6x = 6n2 * m - 3(n2 + n3 - nm - n2) + 2n3 - 3n3 + n = 3 * m * n2 + 3 * m * n - n3 + n
Так как мы решали для n ≤ m то 3n2 * m = ≈ n3, а это значит, что n можно просто перебрать до двух корней кубических.
Асимптотика: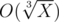 
Задача E.
Решение этой задачи — динамическое программирование.
Пусть froot, mask обозначает количество способов построить дерево с корнем в вершине root на множестве вершин mask с соблюдением всех условий. Для удобства, будем нумеровать вершины с нуля.
Тогда, понятно, что ответ — это ни что иное, как f0, 2n - 1.
Тривиальными будут состояния, где в маске только лишь один единичный бит. В таких случаях froot, mask = 1.
Будем считать эту дп рекурсивно с запоминанием состояний. Чтобы сделать переходы, нам нужно выбрать какую-то маску newMask, которая обязательно является подмаской маски mask. Затем следует перебрать корень newRoot в маске newMask. Так же, для того, чтобы не посчитать одно и то же дерево несколько раз наложим условие на маску newMask. А именно, будем брать только такие маски newMask, в которых старший бит (не отвечающим за root) совпадает со страшим битом (не отвечающий за root) маски mask. После чего, нужно проверить выполнение всех условий на ребра и на lca. Если все хорошо, то обновить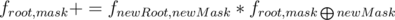 
. Где 
— исключающее или.
Что касается проверки, на lca то ее можно делать за O(N2) — предварительно для каждой пары запомнив lca или в худшем случае за O(Q) просто пробегая по всем парам вершин, для которых какая-то вершина v является lca. В случае с O(Q) состояний достижимых не очень много и поэтому дпшка будет работать довольно быстро.
Асимптотика: O(3N·N3) или O(3N·N·Q)
Auto comment: topic has been updated by Yury_Bandarchuk (previous revision, new revision, compare).
Auto comment: topic has been updated by Yury_Bandarchuk (previous revision, new revision, compare).
sorry, in problem C when you say H_j is H_i right?
Thanks for nice editorial and Nice contest!
Thanks for nice editorial and nice contest :)
Problem A: this line
min(d1, d2) + min(d3, d1+d2) + min(d3+min(d1, d2), max(d1,d2))solves it.what about ? :) min(a,b+c)+min(c,a+b)+min(b,a+c)
even easier :)
I've made a visual explanation for the problem A.
If you guys have any suggestions for improvement, you can comment my explanation right here :)
In the problem D don't we search n in the range [1 X^1/3] and then for each n, m in the range [n,x^1/3]? Is overall complexity O(x^1/3) or O(x^2/3)?
We know that 6x=3n^2*m+3nm+n. If we know n and x we can calculate m.
Sure.Missed it (
Problem C:
I solved it in
nlog(n):I will illustrate on this example:
4 3 4 1 2
(1,3) (2,4) (3,1) (4,2)
and then iterating through this array and know each element should go from where to where (so this segment must be sorted as one partition). For example:
element with value 1 must go from index 3 to 1, so segment(1,3) must be updated.
for Every such segment I either: 1- insert it into a set. 2- if it intercepts with other existing segment in my set, I update both of them into a new segment.
for example: first I insert segment (1,3), then it comes (2, 4). I merge both into one segment which it is (1,4).
lastly, I get the number of segments
segand the total elements they have in themtot, and answer isseg+n-totmy code: 14383376
Hey! I did it in the same fashion :)
I think we solved it the hard way :) there are simpler solutions.
Another nlogn solution 14416195. I think you will find this easier. The code is so short and simple that i don't need to explain what i've done (i guess).
It was my contest time submission 14381758 too. but i resubmitted it to reduce unused codes.
Fastest system testing ever! And super fast editorial. Great job. Ciao.
це була изи катка
Выдели задачи, а то сливаются
Problem D — Spongebob and Squares is a beautiful problem, kudos to the author
I think there is much nicer/easier solution for problem C. I think it work?
Say you have the array elements a1, a2, ..., an. Then, call them sorted be b1 ≤ b2 ≤ ... ≤ bn. Then, for each 1 ≤ i ≤ n, we check if a1 + ... + ai = b1 + ... + bi, and if so, we increment ct++. (If sum are equal, then element must be equal because it is the minimum possible sum). Then ct will be the answer.
Implementation: 14386133
Can you please tell me why the statement " If sum are equal, then elements must be equal" is always true ? Although I noticed this fact with few examples, but I couldn't prove it.
sorry, in problem C when you say H_j is H_i right?
This isn't the only point that confuses me :) I'd actually appreciate if someone wrote a simpler and more detailed explanation for the problem C (at least, by filling in the gap in the logical steps before the sentence 'Firstly, we need to calculate two arrays').
It would also be really great to start seeing the tutorials with pictures. For some reason the pictures are used to describe the problem statements, but they are avoided when they try to explain the solution for those who didn't solve the problem ;)
For problem D: won't the equation be: 6x = 3mn2 + 3mn — n3 + n. I solved using this equation and got accepted. Here is the solution : 14387650
I use the same equation as yours, and I'm confused by the equation in the editorial. Anyone who can explain that? Thanks. :)
but how it is possible??
can you please explain.....
I had got the similar general equation as :
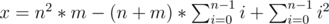
but when I proceed to solve it I got:
6x = 6mn2 — 3(n+m)*(n)*(n-1) + (n)*(n-1)*(2n-1)
I got the above equation after expanding the summations that is sum of k intgers and sum of k squares, here k = n-1.
On further simplification we get the equation I mentioned above :
6x = 3mn2 + 3mn — n3 + n.
thanks adnaan1703
//Solved
My solution for D does not work for certain numbers, but still got AC. (Only sad thing is that I submitted the 'right' solution with an upperbound of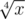
instead of 
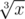, which got hacked. Didn't know that would discard my accepted solution too.)
Let n < m. We can derive that 6x = n(n + 1)(3m + 1 - n). (By the way, you forgot the - n3 in the final formula in the editorial.) What I did: first factorize 6x. Then, generate all divisors of 6x. Now, sort the divisors, and check for each divisor d whether d + 1 is a divisor too. (Thus, whether it equals the next divisor in the list.) If both d and d + 1 are divisors, set n = d and solve for m. If m is an integer, we have found a solution.
The problem is that we can only factor numbers with at most one prime above 106. (Or 107, but that doesn't really help.) The algorithm fails when 6x has two consecutive divisors and two large factors. In particular, this might happen when 6x = 2·3·p·q, and p = q ± 1, p = 2q ± 1, p = 3q ± 1, p = 6q ± 1 or 2p = 3q ± 1. (Although the first case can't happen.) I was to lazy to check each of theses cases separately, but it still passed when I resubmitted it after the contest. I think this solution should have been proven wrong by the system tests, but one can always miss some weird solutions. It was a nice contest anyway!
Solution
I got AC with the same equation without handling any special case...
6x = n(n + 1)(3m + 1 - n)
since n and (n+1) can not have any common factor and 6x/(n*(n+1)) should be integer,
it means 6x should be divisible by n & (n+1) individually...
and as we assume m>=n
it means (3m+1-n)>=2*n+1
hence 6x/(n*(n+1))>=(2*n+1)
so just run a loop for all n with above conditions
code: 14383578
time comp.-> O(cuberoot(x))
Yes, you're right. Since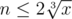
, we only have to know the divisors (or factors) of x up to 2·106. This excludes all my special cases. I clearly wasn't thinking straight yesterday.
in problem B : why don't when i find count of some element b[i] more than 1 immediately print "Ambiguity", is it wrong ?
3 3
1 1 2
1 1 3
If you print "Ambiguity" then there should exist several sequences that satisfy the sequences F and B, but in this case, even though there is ambiguity with the 1's, it's impossible because a 3 never appeared in the sequence F.
How is my logic wrong for A, I only got till pretest 4,I put these 4 values into integers
and then I put these integers into an array and I wrote a for loop to find the minimum value
Hi, I have read some of your submissions. Your logic is right, but your code have some implementation bugs. For example, you store the minimum in an unitialized int variable named 'o'. The default constructor initializes 'o' with some undefined value. That's why your code outputs a 0 in the first case ('o' is initialized with zero). In your last submission, if all the distances are equal, you are not printing anything. You are looking for a number in that array that is strictly less than all the others. Finally, make sure that you are inserting exactly the values (d1+d2+d3), 2*(d1+d3), 2*(d2+d3) and 2*(d1+d2) (I think you are inserting 2*(d1+d2)+d3 instead of d1+d2+d3).
…
Problem D. 6x = -n^3 + 3mn^2 + (3m+1)*n
but how it is possible??
can you please explain.....
What's wrong with my submission? I cant figure it out.. http://mirror.codeforces.com/contest/599/my#
That link takes one to his personal submissions for that contest, not yours.
In Problem B , I did the same thing as mentioned here but its failing in the system tests , Test case #10. Its a pretty large test case so i am able to figure out the bug.
Can anybody tell me whats wrong ? Here's the link to code : http://mirror.codeforces.com/contest/599/submission/14373418
Would be great if anybody could help. Thank You.
It is not ambiguous if there are identical elements in the array b.
For problem D, I assumed that m = (6x + n3 - n) / (3n2 + 3n) is decreasing because data seemed like it. So n's upper bound is when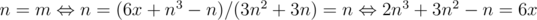
. When 6x gets bigger n gets bigger. So n's upper bound is when 2n3 + 3n2 - n = 6 * 1018 therefore n ≤ 1442249. Fortunately, this got accepted. But after the exam I looked at some m - n graphs for various x values and realized that this is not monotonically decreasing, instead it first goes down, and after n = m it goes up again. I'm wondering if there's any integer (n, m) pairs where n is bigger than the first intersection point (a.k.a my pseudo upper bound). If not, how to prove it?
Graph of the first test case of the problem:
UPD: Nevermind me :D I don't know how I couldn't see n is always bigger than m after intersection (even though m starts to increase again, it increases more slowly compared to n) by looking at that graph.
The problem D.X<=10^18？WA65....
Не понял решение задачи E... За счёт чего работает такой пересчёт динамики, когда мы берём только маски, у которых совпадают старшие некорневые биты? (кажется немного магией :) )
Как получилась формула 6x = 3n2 · m + 3n·m + n ?
У меня получилось: 6x = 3n2·m - n3 + 3n·m + n (AC: 14396538)
problem B is failing on test 20 and i can't figure out the bug. can anyone help me ?
here's my code 14400028
You can have situation when you say: "Ambiguity" and return 0, but after your answer you have f[i] that not exist... For example: n = 4, m = 2, f = {1, 1, 3, 4} b = {1, 50} Answer: Impossible
you should test that the solution "possible" before saying "Ambiguity" because you say that there is many solution but actually there is no solution
correct me if i'm wrong
i'm checking like this
1- if the number doesn't exists in (F) print impossible close the program, else continue
2-if the number exists more than once in (F) print ambiguity close program ,else continue
3- if the number passes all the above then it's possible to find a solution ,store number in an array
2nd point is wrong.
If you say there is ambiguity, then there should be several ways to create a sequence A that satisfies the sequences F and B.
Check this case
3 3
1 1 2
1 1 3
In your 2nd point, you can't close the program if you get ambiguity, as it is possible you get "Impossible" later. An impossible solution also may have ambiguities.
So keep a flag for ambiguity. If you find solution is not "impossible", then and only then print ambiguity, and else the answer.
About problem C:
I got wrong answer in test case 7 which is:
25
1 2 3 4 4 4 4 4 4 4 2 3 5 5 7 9 8 5 10 12 15 12 100500 800600 228228228
My output: 13 Jury's output: 12
The maximum number of blocks was asked to find out. In this test case my partition is: [1][2][3 4 4 4 4 4 4 4 2][3][5][5][7 9 8 5][10][12][15 12][100500][800600][228228228] -->> total 13 blocks.
Could anyone tell me where I am doing mistake?????
In your answer [1][2][3 4 4 4 4 4 4 4 2][3][5][5][7 9 8 5][10][12][15 12][100500][800600][228228228]
The 3rd and 4th block have to be merged as 3 is less than 4. So finally you will have 12 blocks, which is the answer.
[1][2][3 4 4 4 4 4 4 4 2 3][5][5][7 9 8 5][10][12][15 12][100500][800600][228228228]
I was making the same mistake you were. Let us see what that mistake is with an example.
4 3 6 1 2 5
I was finding for every element, the last index among all elements which are less than it. So for 4, I find that 2 is last element less than it, so I formed the blocks
[4 3 6 1 2][5]. But this is incorrect.
What I didn't consider is that in the newly formed block there maybe some element greater than the start of the block,, and that will introduce more inversions. So here, 6 is greater than 4, so 5 also has to be included in the block. Hence final block is [4 3 6 1 2 5]
Hope you get the point.
in PROBLEM B
I adjusted my code and it's failing on test 28 .the weird thing is that test 28 gives me the correct answer when i run it on my PC but gives a completely different answer on the judge's system. here's the submission 14411133
In your code, you need to set your "bool exists[]" array to zero. Since you are not doing that, your bool array is getting garbage values and hence your answer is wrong.
So, either declare the array as global(which automatically sets it to zero), or do a memset, or go through the array in a loop and set all values to zero.
Here is the AC submission: AC
D Getting 6x = 6n2 * m - 3(n2 + n3 - nm - n2) + 2n3 - 3n3 + n = 3 * m * n2 + 3 * m * n - n3 + n wrong? Is this? Getting 6x = 6n2 * m - 3(mn2 + n3 - nm - n2) + 2n3 - 3n3 + n = 3 * m * n2 + 3 * m * n - n3 + n
Can someone explain E in more detail ??
DELETED
deleted
deleted
Дискриминация индусов.
deleted
DELETED
Can someone please give the necessary resource links(blogs,tuts etc) for understanding problem E as could not understand it
Hey, I was upsolving some problems and one of them was E of this contest.
I liked the problem and after reading the editorial and some silly mistakes in the implementation I got accepted and feel that I learned something, but there's something I don't understand in the editorial, the time complexity.
I understand how to check the fulfillment of the conditions before a transition in O(N3) or O(N·Q) but I don't understand where does the O(3N) come from.
Could anyone give me an explanation or at least some hints about the 3N? ;)
Thanks :)
Although I'm a beginner , luckily I know why 3^N.( my English is poor, sorry ) All of the states is 2^N, that is no problem. For every state that has i of 1 in its bits( 11101 is 4, 11001 is 3, 10011 is 3) the number of submasks of it is 2^i(other bit is 0) so the equation is C(i,N)*2^i ( 0 < i <= N ) so it's 3^N This thing has also been used in the solution to Steiner Tree, maybe you can google it. Hope helpful to you.
tfw you solve problem C with sieve of eratosthenes
Can Anyone help me in understanding the testcases of problem B.