Блог пользователя ilyaraz

Две задачи по терверу с неожиданными ответами
Автор ilyaraz, 13 лет назад, По-русски

Вот две задачи по терверу, которые сами по себе довольно простые и не неожиданные, но в них на мой вкус очень забавные ответы. Итак...

1. Представьте себе, что мы хотим сгенерировать случайный бит следующим странным способом. Возьмем очень-очень большое натуральное n и случайный двудольный граф, в каждой доле которого по n вершин. Посчитаем в нем количество совершенных паросочетаний (наборов из n ребер, которые не имеют общих концов). Четность этого количества и будет нашим битом. Какова вероятность, что этот бит будет равен нулю?

2. Представьте себе, что у нас есть n корзинок, в которые мы случайно бросаем шары. Мы продолжаем процесс, пока в каждой корзинке не будет по крайней мере m шаров. Сколько в среднем шаров мы бросим? Интересует ответ с точностью до константы. Например, хорошо известно, что если m = 1, то в среднем мы бросим 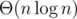шаров.

  • Проголосовать: нравится
  • +42
  • Проголосовать: не нравится

13 лет назад, # |
← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится

1. Четность числа паросоч. в случайном двудольном графе будет равна определителю случайной матрицы над поэтому ответ будет 0 с вероятностью того, что n случайных n-мерных векторов над линейно зависимы. А эта вероятность  < 2n· 1 / 2n. Так что при оч. большом n ответ почти 0.
→ Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    А откуда такая оценка взялась?
    → Ответить
    • 13 лет назад, # ^ |
      ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

      Вектора зависимы если все попали в (n - 1)-мерное подпр-во. Вероятность, что случайный вектор попадет в задданное (n - 1)-мерное подпр-во = 1 / 2. Всего 2n (n - 1)-мерных подпр-в.
      → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +10 Проголосовать: не нравится
    Ну раз уж такое дело, ничто не мешает точную формулу написать:


    PS. А что случилось с командой \frac{}{} ?
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Ага, у этого выражения есть предел при n → ∞, который, вероятно, иррационален. По-моему, забавно, что ответ не 0, не 1 и не 0.5.
      → Ответить
      • 13 лет назад, # ^ |
        ← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится

        а можно как-то выразить произведение элементов вида (2^i -1) от 1 до n ?
        → Ответить
        • 13 лет назад, # ^ |
          ← Rev. 2   Проголосовать: нравится +8 Проголосовать: не нравится

          С ростом n это произведение будет иметь все больше и больше простых делителей. Не уверен, но по-моему это значит, что формулы с фиксированным числом множителей не существует.
          → Ответить
13 лет назад, # |
  Проголосовать: нравится +8 Проголосовать: не нравится
В первой задаче вероятность получилась примерно 0,711211. А есть точная формула для ответа?
→ Ответить
13 лет назад, # |
  Проголосовать: нравится +10 Проголосовать: не нравится
Очень интересно было бы узнать решение задачи, получаемой из второй заменой "пока в каждой" на "пока хотя бы в одной". Например, для m=2 ответ пропорционален sqrt(n) (парадокс дней рождения).
→ Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +5 Проголосовать: не нравится
    А типа задачу из поста вы уже решили? :)
    → Ответить
  • 13 лет назад, # ^ |
    ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

    Мне кажется, что ответ на вашу задачу , если m фиксированное. Тут-то как раз нету ничего неожиданного.
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится +6 Проголосовать: не нравится
      Ну если в вашей задаче зафиксировать m, то ответ будет всегда одинаков, и он указан в условии. Нет разве? :)
      → Ответить
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Первую задачу иногда дают в яндексе на собеседовании, в целом она довольно известная.
Во второй задаче (в исходном варианте) у меня получилось \Theta(n\cdot (\log n + m\log m))
→ Ответить
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
оценкой вероятности, что вероятность того, что событие еще не произошло <= 1/2
→ Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    Я умею доказывать верхнюю оценку, которая меньше твоей нижней. Не знаю уж, у кого ошибка.
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      у меня довольно много вычислений, поэтому могу написать только план:

      ответ (обозначим его k) больше n\log n, это из m = 1 легко извлечь
      ответ больше nm\log m, т.к. вероятность того, что в первой ячейке меньше m должна быть меньше 1/2, т.е. C_{k}^{m-1}(n-1)^{k-m+1}/n^k <1/2
      в конечном итоге получим exp(k/n) > С(m)\cdot (k/n)^{m} ч.т.д
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        Откуда это взялось?
        > вероятность того, что в первой ячейке меньше m должна быть меньше 1/2
        → Ответить
        • 13 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится
          если она >1/2, то с вероятностью хотя бы 1/2 все закончится позже, т.е. матожидание не меньше k/2
          → Ответить
          • 13 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится
            я нашел у себя ошибку, теперь у меня n(m+ \log n)
            → Ответить
            • 13 лет назад, # ^ |
                Проголосовать: нравится 0 Проголосовать: не нравится
              Ну да, теперь нижняя оценка очевидна. А как верхняя доказывается?
              → Ответить
              • 13 лет назад, # ^ |
                  Проголосовать: нравится +5 Проголосовать: не нравится
                почти также, только надо домножить на n, чтобы заведомо покрыть все ячейки, а потом оценить количество шагов, которое уменьшает вероятность в два раза. Там будет линейно, потом остается только свернуть убывающую геом. прогрессию с линейным множителем в константу. Кстати, эта стандартная схема не работает в задаче, которую поставил Walrus
                → Ответить
                • 13 лет назад, # ^ |
                    Проголосовать: нравится +1 Проголосовать: не нравится
                  Да, наверное можно и так. Есть решение в одну строчку, которое использует неравенство Чернова.
                  → Ответить
                  • 13 лет назад, # ^ |
                      Проголосовать: нравится 0 Проголосовать: не нравится
                    с помощью Чернова понятно только как верхнюю оценку доказывать
                    → Ответить
                    • 13 лет назад, # ^ |
                        Проголосовать: нравится +5 Проголосовать: не нравится
                      А нижняя и так очевидна: ясно, что ответ не меньше и не меньше Ω(nm).
                      → Ответить