akashdeep's blog

ACM-ICPC Asia-Amritapuri Onsite Mirror Contest 2015 on CodeChef
By akashdeep, history, 9 years ago, In English

For the first time in the history of Indian ACM ICPC, a mirror contest will be hosted on CodeChef for Amritapuri regionals at http://www.codechef.com/AMR15MOS.

Time: 21st December 2015 (1000 hrs) to (1500 hrs). (Indian Standard Time — +5:30 GMT) — Check your Time zone.

Details: http://www.codechef.com/AMR15MOS/

Registration: It will be a team contest. You need to register your team here

New users please register here

The contest is open for all and those, who are interested, are requested to have a CodeChef userid, in order to participate.
  • Vote: I like it
  • +24
  • Vote: I do not like it

Comments Comments (47)
| Write comment?
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can view the live blog here and a live scoreboard here.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it +15 Vote: I do not like it

    the scoreboard seems to have become static.Whenever I refresh it always shows "time left:3:49 :53".Is anybody else also facing the same issue? further no updates have been there on the twitter blog for the last 40 minutes whereas previously it was updated every 10 minutes.

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

I can't submit problem AMLPALIN — "submit" button moves me to the very same page.

Also there are only 8 problems in online mirror, while there are 10 of them in live standings.

Thanks, it seems that now everything is fine.

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

404 error now , cant load page

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Onsite: https://www.codechef.com/ACM15AMR

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve Magical Matrix?

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Who Won in the regionals ?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there going to be an editorial?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve Similar Strings?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it +1 Vote: I do not like it

    DP[i][j] — number of pairs of similar strings where first string has length i and second string has length j.

    Create another table S[i][j] — number of pairs of similar string where first string has length at most i and second string has length at most j (it will be partial sum over DP table).

    Now you can say that DP[i][j]=S[i-1][j-1]*25+26 — you can either pick pair of equal strings where first string has length at most i-1 and second string has length at most j-1, and add same letter at the end of both strings (25 comes here because added letter should be different from last letter of these strings), or you can pick pair of strings consisting of single character (26 ways, depending on character you are going to use).

    After precomputing both tables you can answer query in O(1) — result will be simply S[N][N].

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      This problem can also be solved using pure combinatorics.

      Notice that for each string of length 'n', the length of reduced string (say 'i') lies in the range from 1 to n (1 <= i <= n).

      Number of reduced strings of length 'i' = 26 * (25 ^ (i-1) ). (26 choices for the first character, and 25 for every other position, because every character has to be different from the last — follows from the definition of reduced string).

      Number of strings (of length 'n') reducing to a reduced-string of length 'i' is the same as distributing (n-i) identical objects among i boxes = C[(n-i)+i-1][i-1].

      Square this value (remember we have to count number of pair of such strings), multiply with 26 * (25 ^ (i-1)) and add to ans[n] for each 1 <= i <= n.

      Maintain an accumulated sum array, and you are good to go! Code for reference.

      → Reply
»
9 years ago, # |
  Vote: I like it +20 Vote: I do not like it

COPRIMES is a great problem :)!

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How do you solve it? I can't even think how to solve it if we need to find the answer for a fixed L,R

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it +13 Vote: I do not like it

      Step 1: Use standard method of inclusion-exclusion over square-free numbers to solve this problem: http://main.edu.pl/en/archive/pa/2011/lic (this problem is basically equivalent to one query in this problem).

      Step 2: We definitely need to solve this problem offline. Assume that K is fixed for all queries. Think about how can you apply Mo's algorithm.

      Step 3: Think how can you deal with changing values of K. How can we omit iterating over all square-free numbers for every query?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Can you explain how to do the step 3, in the contest we had got the ideas for the first 2 steps but couldn't come up with any good method for varying k as the time was running out.

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Let i be a square-free number and cnt[i] denote the number of elements in current interval which are multiplies of i (you have probably already defined that in step 2). Let cnt_cnts[i] = sum_{cnt[x] = i} mu(x). How can you use that array to retrieve an answer. What is the sum of all values of cnt[i] and how can you use that to make suggested approach fast enough?

          → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        For step 2 I was thinking of the following approach but don't think it is fast enough:

        When adding/removing an element 'x' during Mo's algo, for each square free number 'i' that divides 'x', I update cnt[i] i.e. number of numbers divisible by 'i' in the current range.

        When adding/removing an element, the answer for the new range will be old_ans +/- C(sum(cnt[i]*mu(i)), k-1) where i is a square free number that divides 'x'

        But since a number <= 10^5 can have as many as 64 square free factors, it suggests a worst case complexity of 64*N*sqrt(N)

        What is your approach?

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it +6 Vote: I do not like it

          You can find a short description + solution in C++ here

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            So is the final complexity is ?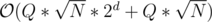

            If yes then why do you say "So we have achieved O(Q*B*2^d) solution here, which won’t pass in time yet"

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              9 years ago, # ^ |
                Vote: I like it +3 Vote: I do not like it

              In the final answer, the complexity is O(Q*B*2^d) additions + O(Q*B) multiplications. In the former solution number of multiplications itself were O(Q*B*2^d).

              Generally multiplications are much slower (around ~20 times, maybe) than additions.

              → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Step 1: Use standard method of inclusion-exclusion over square-free numbers to solve this problem: http://main.edu.pl/en/archive/pa/2011/lic — Can you explain how to solve this using inclusion exclusion?

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +32 Vote: I do not like it

    I am the setter of this problem, Thanks :)

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Is problem cat and mouse a graph problem + binary search?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    Yes. Binary search + bipartite matching.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Great! Now, all I have to do is learn what in good heavens bipartite matching is !! :/

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Could you elaborate further?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it +9 Vote: I do not like it

        Sure. We binary search on the answer. Assume that you have some value "limit" (which is the mid in your binary search) which is the maximum distance between any (cat, mouse) pair in your chosen set. Now you have to verify whether it is possible to select a set of animals of size at least k and satisfying max distance <= limit.

        Construct the graph as a bipartite one, with cats and mice on either side. For a particular cat vertex, add an edge to each mouse vertex if the distance between them is >= limit. Basically, an edge denotes an incompatible pair (for each edge, you can select atmost one of its endpoints, never both). Now the max no of animals you can select in this case is the maximal independent set of this graph. But MIS = total vertices — min vertex cover.

        Total vertices = 2*n and Min vertex cover = max bipartite matching (Konig's theorem)

        So for each value of "limit", you check whether it is possible or not and you adjust the low and high of the binary search accordingly.

        → Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

How to solve the problem COINS?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

how to solve jump on buildings?? any hints??

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Between indices i (starting pt.) and j (2nd point on which we jumped) store the maximum no. of jumps you can make in dp[i][j].

    dp[i][j] = ( Hi>Hj ) ? ( 1+dp[j][i-1] ) : 0

    Answer for any index i will be max(dp[i][k] where k varies from 1 to n)

    To ensure sub state of dp has been calculated for calculating answer for any state ... compute the answer in ascending order of heights of building i.e first compute dp[i][j] for j=1 to n and i as the index of height of smallest building and so on !

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Logic for approaching git problem ??

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Some hints :

    Build trie for simulating the entire directories.

    Use dynamic programming [current_node][0/1]. 0 means the node is excluded, 1 means it is included.

    Do DP from the leaf.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ok thanks Will go learn tries and try implementing

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Didn't get the rule --"There will be no file — directory conflict. e.g. consider /a/b/c and /a/b. Here b is both a file and a directory."

      what should be the ans for foll: (if such a case fits the rule)

      stage /a/b stage /a/b/c unstage /a/b/d unstage /a/b/e

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Any hints on how to solve the problem: Jump on Buildings. I have O(N^3) solution but that would timeout.

Thanks

→ Reply