Всем привет!
Осенью на физтехе проходили сборы по программированию Moscow International Workshop ACM ICPC. На них мне довелось прочесть лекцию по суффиксным структурам (на самом деле, были затронуты только суффиксное дерево и суффиксный автомат). В связи с этим я хотел бы предоставить вашему вниманию конспект лекции. Собственно, вот русская и английская версии. Приятного просмотра и счастливого Нового года :)
P.S. любая критика, предложения, пожелания и вопросы всячески приветствуются.
P. P. S. Я попытался достаточно подробно описать доказательство линейности работы, но, скорее всего, оно до сих пор тяжело воспринимается. Вы получите +100 единиц кармы, если разберётесь в нём и предложите более простой для понимания вариант :)
UPD: Спасибо Burunduk1 за помощь в форматировании кода :)
UPD2: См. также статью на Википедии по этой теме. Я являюсь основным автором текущей (29 октября 2021) версии статьи.











Hi, first of all thanks a lot, and secondly would you mind tagging this with
tutorialso it would be easier to search for in the future? I looked at the notes, and they are definitely not to be missed out on!Here you go :)
[DELETED]
Ты действительно думаешь, что я их не читал? :)
А ты хотя бы открывал статью про Укконена? Там сам алгоритм считай, что не описан.
А есть ли в природе еще конспекты типо таких?
было бы неплохо если бы кто-нибудь поделился еще какими-нибудь конспектами.
I was reading your excellent tutorial and got confused by one sentence(paragraph). Could you plz explain it to me?
Pretty easy to understand that in case of suffix automaton right conext X(a) of string a has mutual correspondence with the set of right positions of occurrences of the string a in the string s. Indeed, if ax is accepted by automaton, that is, it is a suffix of s, then s = yax, and the string x can be matched with position |s| − |x| − 1. Thus, each state of the automaton accepts strings with the same set of right positions of occurrences in s and vice versa all strings with such set of positions is accepted by this state.
I couldn't understand the first sentence clearly. Thanks for helping.
To each element in right conext you can associate the occurence in string. And vice versa.
For example, let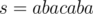 . We can find that
. We can find that 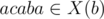 and associate it with first occurence of ab ( ab acaba). And for second occurence there is element in right context:
and associate it with first occurence of ab ( ab acaba). And for second occurence there is element in right context: 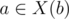 (abac ab a).
(abac ab a).
I understand the example and sort of getting your idea, but what does "mutual correspondence" mean?
It means bijection :)
do I need to work more on this paragraph if I can understand your example but not really for the text?
Maybe no. Try going on without it and return to it if you have some difficulties maybe
adamant, есть ли какие-либо задачи, которые решает суффиксное дерево, но не может решить или решает хуже суффиксный автомат?
Hi everyone! I'm sorry that Google Drive links got broken. I've updated this entry with new links which should work now. On a side note, these lecture notes are quite old and might be somewhat messy, therefore I strongly encourage to use Wikipedia article on this topic. I am the main author of its current version.
--
Всем привет! Извиняюсь, что ссылки на Google Drive сломались. Я обновил пост и добавил работающие ссылки. Тем временем, хочу отметить, что материал тут довольно старый и местами трудный к восприятию, поэтому я предлагаю также ознакомиться со статьёй на Википедии по этой теме. Я -- основной автор текущей версии статьи.
Ссылка на википедию в посте тоже сломана.
Спасибо, исправил.