616A - Сравнение длинных чисел

Замечу, что в этой задаче решения, использующие стандартные типы длинной арифметики (класс BigInteger в Java, стандартные длинные числа в Pyhon) не должны проходить. Это связано с тем, что они хранят число не в десятичной системе счиления и соответственно при создании длинного числа происходит его конвертация из десятичной системы счисления, которая является тяжёлой операцией и работает обычно за O(n²), где n — длина числа.

Для решения задачи можно просто добавить лидирующих нулей к более короткому числу, а далее сравнить, получившиеся строки в лексикографическом порядке (алфавитном).

С++ solution

Python solution

Сложность: O(n).

616B - Ужин с Наташей

В этой задаче нужно было сначала найти в каждой строке минимум, а далее взять максимум, получившихся минимумов. Это соответствует стратегии Павла и Наташи.

C++ solution

Сложность: O(nm).

616C - Лабиринт

Давайте сначала пронумеруем все компоненты связности, запомним для каждой её размер, а также для каждой свободной клетки запомним номер её компоненты. Это можно сделать с помощью одного обхода в глубину. Теперь ответ для непроходимой клетки будет равен единице плюс размеры всех соседних различных компонент. Соседних в смысле компонент всех соседних клеток (в общем случае четырёх).

C++ solution

Сложность: O(nm).

616D - Наидлиннейший k-хороший подотрезок

Эту задачу мы решили дать поскольку на страницах Codeforces часто видим вопрос "Что такое метод двух указателей?". Эта задача является типичным примером задачи, решаемой этим методом.

Будем искать для каждой левой границы l наибольшую границу r такую, что отрезок (l, r) k-хороший. Заметим следующее: если некоторый отрезок (l, r) k-хороший, то отрезок (l + 1, r), тоже является хорошим. Таким образом, поиск максимальной правой границы для левого конца l + 1 мы можем начинать с максимальной правой границы для левого конца l. Далее просто будем поддерживать в массиве cnt_x для каждого числа x количество его вхождений в текущий отрезок (l, r), а также количество различных чисел. Будем пытаться двигать правую границу пока можем, далее двигать на единицу левую границу. Итого два указателя l, r вместе передвинутся 2n раз.

C++ solution

Сложность: O(n).

616E - Сумма остатков

К сожалению в этой задаче в моём решении происходило переполнение. Ошибка была исправлена во время соревнования, надеюсь это не сильно убавило вам удовольствие от решения этой задачи, поскольку она мне кажется очень интересной и красивой (идея решения, конечно, является известной для искушённых пользователей).

Сначала преобразуем сумму, которую нужно посчитать 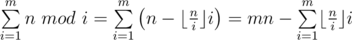. Также заметим, что последнюю сумму можно суммировать до min(n, m), поскольку при i > n все слагаемые будут равны 0.

Заметим, что в последней сумме либо 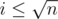, либо 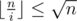. Будем аккуратно суммировать эти два случая так, чтобы ничего не посчитать два раза. Первую сумму посчитать легко, просто нужно пройти циклом по всем таким i. Вторую сумму будем считать отдельно для всех различных значений 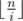. Для этого во-первых нужно определить при каких i значение 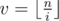будет достигаться. Легко видеть, что это полуинтервал 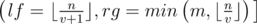. Также нужно понять, что сумма вторых сомножителей в 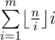при постоянном первом сомножителе легко считается за константное время — это просто сумма арифметической прогрессии 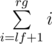. Таким образом решение работает за .

С++ solution

Сложность: .

616F - Дорогие строки

Эта задача была предложена и подготовлена Григорием Резниковым vintage_Vlad_Makeev. Его решение использовало суффиксный массив.

Вообще задача является типичным примером задачи на суффиксную структуру. Четверо из пяти участников сдавших задачу в основное время соревнования использовали суффиксный автомат, один использовал суффиксное дерево. Моё решение использовало суффиксное дерево, поэтому я расскажу решение с деревом (оно мне кажется простым, не считая построения самого дерева).

Построим новую строку, расположив друг за другом все строки из набора, разделив их различными разделителями. Количество разделителей порядка O(n), поэтому алфавит в суффиксном дереве тоже порядка O(n). Соответственно нужно использовать map<int, int> для хранения дерева и в асимптотике выходит O(logn). Построим для получившейся строки суффиксное дерево. Поставим в соответствие каждому разделителю строку слева от него. Теперь запустим на этом дереве обход в глубину, который никогда не переходит через разделитель и возвращает сумму цен строк, соответствующих множеству разделителей в поддереве вершины обхода в глубину. Легко видеть, что ответ это просто произведение глубины текущей вершины на сумму в поддереве этой вершины.

С++ solution

Сложность: O(nlogn).