Edvard's blog

Editorial of Educational Codeforces Round 5
By Edvard, history, 9 years ago, translation, In English

616A - Comparing Two Long Integers

Note that solutions in Java with BigInteger class or input() function in Python2 will fail in this problem. The reason is the next: standard objects stores numbers not in decimal system and need a lot of time to convert numbers from decimal system. Actually they are working in O(n2), where n is the legth of the number.

To solve this problem you should simply read the numbers to strings and add leading zeroes to the shorter one until the numbers will be of the same length. After that you should simply compare them alphabetically.

С++ solution

Python solution

Complexity: O(n).

616B - Dinner with Emma

Firstly you should find the minimum value in each row and after that you should find the maximum value over that minimums. It's corresponding to the strategy of Jack and Emma.

C++ solution

Complexity: O(nm).

616C - The Labyrinth

Let's enumerate all the connected components, store their sizes and for each empty cell store the number of it's component. It can be done with a single dfs. Now the answer for some impassable cell is equal to one plus the sizes of all different adjacent connected components. Adjacent means the components of cells adjacent to the current impassable cell (in general case each unpassable cell has four adjacent cells).

C++ solution

Complexity: O(nm).

616D - Longest k-Good Segment

This problem is given because on the Codeforces pages we often see questions like "What is the method of the two pointers?". This problem is a typical problem that can be solved using two pointers technique.

Let's find for each left end l the maximal right end r that (l, r) is a k-good segment. Note if (l, r) is a k-good segment then (l + 1, r) is also a k-good segment. So the search of the maximal right end for l + 1 we can start from the maximal right end for l. The only thing that we should do is to maintain in the array cntx for each number x the number of it's occurrences in the current segment (l, r) and the number of different numbers in (l, r). We should move the right end until the segment became bad and then move the left end. Each of the ends l, r will be moved exactly n times.

C++ solution

Complexity: O(n).

616E - Sum of Remainders

Unfortunately my solution for this problem had overflow bug. It was fixed on contest. Even so I hope you enjoyed the problem because I think it's very interesting.

Let's transform the sum 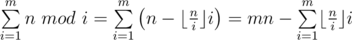. Note that the last sum can be accumulated to only value min(n, m), because for i > n all the values will be equal to 0.

Note in the last sum eithe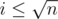r or 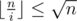. Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all 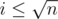. We will accumulate the second sum independently for all different values 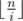. Firstly we should determine for which values i we will have the value 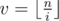. Easy to see that for the values i from the interval 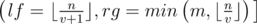. Also we can note that the sum of the second factors in 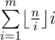with fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression 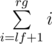. So we have solution with complexity .

С++ solution

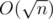Complexity: .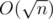

616F - Expensive Strings

This problem was prepared by Grigory Reznikow vintage_Vlad_Makeev. His solution uses suffix array.

This problem is a typical problem for some suffix data structure. Four competitors who solved this problem during the contest used suffix automaton and one competitor used suffix tree. My own solution used suffix tree so I'll describe solution with tree (I think it's simple except of the building of the tree).

Let's build the new string by concatenation of all strings from input separating them by different separators. The number of separators is O(n) so the alphabet is also O(n). So we should use map<int, int> to store the tree and the complexity is increased by O(logn). Let's build the suffix tree for the new string. Let's match all the separators to the strings from the left of the separator. Let's run dfs on the suffix tree that doesn't move over separators and returns the sum of the costs of the strings matched to the separators from the subtree of the current vertex. Easy to see that we should simply update the answer by the product of the depth of the current vertex and the sum in the subtree of the current vertex.

С++ solution

Complexity: O(nlogn).

  • Vote: I like it
  • +63
  • Vote: I do not like it

Comments Comments (30)
| Write comment?
»
9 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

the equation in second sentence in solution of problem E why m*(m+1)/2 ?? I think it should m*n

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E is indeed a nice one I think, which helps find what a stupid ACMer I am. :P But fortunately, I learn a lot from this one. Thank you!

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E was a better modified version to the problem www.spoj.com/problems/SUMPRO

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem F could be done with suffix array or just with suffix automaton or with the suffix tree?

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can someone explain the solution for problem F using suffix array.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem C java tle

http://pastebin.com/E91JSjsV

my soln seems to be same as the one in editorial any inputs?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think, it's because of adding strings when constructing answer (lines 56 & 86). As I know, it's expensive operation :) For example, try to add 1000000 digits to string.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Used printwriter in place of system.out Passed 13-14-15 Tle at 16 now Any other way to o/p large strings in java ?(with newline) Or create them without concatenation?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You can use StringBuilder. I believe that it's much faster than simple String concatenation.

        StringBuilder sb = new StringBuilder();
sb.append(appendWhatYouNeedHere);
        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem D can also be solved by a Regular sliding Window technique and Binary search on the length.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I solved it using just sliding window technique, no binary search

    → Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Someone please guide me where should I learn Suffix arrays and Suffix trees from.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Somebody can please clarify the meaning of this line of code of the solution for E?

inline li sum(li n) { return mul(mul(n, n + 1), (mod + 1) / 2); }

I didn't understand why you multiply n(n+1) * (mod+1)/2 [the mod part]. Using n*(n+1)/2 and then aplying % mod would be equivalent?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it +1 Vote: I do not like it

    (mod + 1) / 2 is inverse element for 2 in the field modulo mod.

    UPD: For odd mod.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you so much! I'm going to search and try learn more about that

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone tell me what is the difference between declaring a function as 'inline void' instead of just 'void'? Thank you.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My code for problem A: http://pastebin.com/fYTUiV1P

I got TLE on problem A on test 20. Can somebody help me with that? I used PrintWriter and BufferedReader in my code but still got TLE.

Thank you so much.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Your algorithm is O(N^2) because insert in StringBuilder can't possibly work faster than O(N).

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Nice trick To calculate (x/2)%mod, I used to think inverse modulo would be the only way to do this, but this can be easily fashioned as ""(x*(mod+1)/2)%mod"", as (mod+1)%mod = 1 and mod is an odd prime number.

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I followed the problem B's editorial, but still got wrong answer in test case 9. could anybody please verify? (http://mirror.codeforces.com/contest/616/submission/15829627)

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +12 Vote: I do not like it

    Swap n and m in array declaration.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

How can I solve F using Suffix automaton? note: I don't know the code all people used to solve this problem, I only know the traditional one found on e_max.

→ Reply
»
5 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

has anyone did D using binary search? i am getting TLE for case 12.

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

First 4 problems were easy

→ Reply