616A - Comparing Two Long Integers
Note that solutions in Java with BigInteger class or input() function in Python2 will fail in this problem. The reason is the next: standard objects stores numbers not in decimal system and need a lot of time to convert numbers from decimal system. Actually they are working in O(n2), where n is the legth of the number.
To solve this problem you should simply read the numbers to strings and add leading zeroes to the shorter one until the numbers will be of the same length. After that you should simply compare them alphabetically.
Complexity: O(n).
616B - Dinner with Emma
Firstly you should find the minimum value in each row and after that you should find the maximum value over that minimums. It's corresponding to the strategy of Jack and Emma.
Complexity: O(nm).
616C - The Labyrinth
Let's enumerate all the connected components, store their sizes and for each empty cell store the number of it's component. It can be done with a single dfs. Now the answer for some impassable cell is equal to one plus the sizes of all different adjacent connected components. Adjacent means the components of cells adjacent to the current impassable cell (in general case each unpassable cell has four adjacent cells).
Complexity: O(nm).
616D - Longest k-Good Segment
This problem is given because on the Codeforces pages we often see questions like "What is the method of the two pointers?". This problem is a typical problem that can be solved using two pointers technique.
Let's find for each left end l the maximal right end r that (l, r) is a k-good segment. Note if (l, r) is a k-good segment then (l + 1, r) is also a k-good segment. So the search of the maximal right end for l + 1 we can start from the maximal right end for l. The only thing that we should do is to maintain in the array cntx for each number x the number of it's occurrences in the current segment (l, r) and the number of different numbers in (l, r). We should move the right end until the segment became bad and then move the left end. Each of the ends l, r will be moved exactly n times.
Complexity: O(n).
616E - Sum of Remainders
Unfortunately my solution for this problem had overflow bug. It was fixed on contest. Even so I hope you enjoyed the problem because I think it's very interesting.
Let's transform the sum 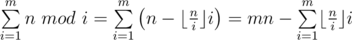 . Note that the last sum can be accumulated to only value min(n, m), because for i > n all the values will be equal to 0.
. Note that the last sum can be accumulated to only value min(n, m), because for i > n all the values will be equal to 0.
Note in the last sum either 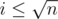 or
or 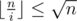 . Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all
. Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all 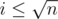 . We will accumulate the second sum independently for all different values
. We will accumulate the second sum independently for all different values 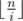 . Firstly we should determine for which values i we will have the value
. Firstly we should determine for which values i we will have the value 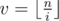 . Easy to see that for the values i from the interval
. Easy to see that for the values i from the interval 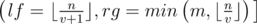 . Also we can note that the sum of the second factors in
. Also we can note that the sum of the second factors in 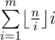 with fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression
with fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression 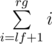 . So we have solution with complexity
. So we have solution with complexity 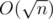 .
.
Complexity: 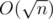 .
.
616F - Expensive Strings
This problem was prepared by Grigory Reznikow vintage_Vlad_Makeev. His solution uses suffix array.
This problem is a typical problem for some suffix data structure. Four competitors who solved this problem during the contest used suffix automaton and one competitor used suffix tree. My own solution used suffix tree so I'll describe solution with tree (I think it's simple except of the building of the tree).
Let's build the new string by concatenation of all strings from input separating them by different separators. The number of separators is O(n) so the alphabet is also O(n). So we should use map<int, int> to store the tree and the complexity is increased by O(logn). Let's build the suffix tree for the new string. Let's match all the separators to the strings from the left of the separator. Let's run dfs on the suffix tree that doesn't move over separators and returns the sum of the costs of the strings matched to the separators from the subtree of the current vertex. Easy to see that we should simply update the answer by the product of the depth of the current vertex and the sum in the subtree of the current vertex.
Complexity: O(nlogn).







