620A - Professor GukiZ's Robot
Easy to see that the answer is max(|x1 - x2|, |y1 - y2|).
Complexity: O(1).
620B - Grandfather Dovlet’s calculator
Let's simply iterate over all the values from a to b and add to the answer the number of segments of the current value x. To count the number of segments we should iterate over all the digits of the number x and add to the answer the number of segments of the current digit d. These values can be calculated by the image from the problem statement and stored in some array in code.
Complexity: O((b - a)logb).
620C - Pearls in a Row
Let's solve the problem greedily. Let's make the first segment by adding elements until the segment will be good. After that let's make the second segment in the same way and so on. If we couldn't make any good segment then the answer is - 1. Otherwise let's add all uncovered elements at the end to the last segment. Easy to prove that our construction is optimal: consider the first two segments of the optimal answer, obviously we can extend the second segment until the first segment will be equal to the first segment in our construction.
Complexity: O(nlogn).
620D - Professor GukiZ and Two Arrays
We can process the cases of zero or one swap in O(nm) time. Consider the case with two swaps. Note we can assume that two swaps will lead to move two elements from a to b and vice versa (in other case it is similar to the case with one swap). Let's iterate over all the pairs of the values in a and store them in some data structure (in C++ we can user map). Now let's iterate over all the pairs bi, bj and find in out data structure the value v closest to the value x = sa - sb + 2·(bi + bj) and update the answer by the value |x - v|. Required sum we can find using binary search by data structure (*map* in C++ has lower_bound function).
Сложность: O((n2 + m2)log(n + m)).
620E - New Year Tree
Let's run dfs on the tree and write out the vertices in order of their visisiting by dfs (that permutation is called Euler walk). Easy to see that subtree of any vertex is a subsegment of that permutation. Note that the number of different colours is 60, so we can store the set of colours just as mask of binary bits in 64-bit type (*long long* in C++, long in Java). Let's build the segment tree over the permutation which supports two operations: paint subsegment by some colour and find the mask of colours of some segment.
Complexity: O(nlogn).
620F - Xors on Segments
We gave bad constraints to this problem so some participants solved it in O(n2 + m) time.
Note that 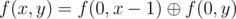 . The values f(0, x) can be simply precomputed. Also you can notice that the value f(0, x) is equal to x, 1, x + 1, 0 depending on the value x modulo 4.
. The values f(0, x) can be simply precomputed. Also you can notice that the value f(0, x) is equal to x, 1, x + 1, 0 depending on the value x modulo 4.
Let's use Mo's algorithm: we should group all the queries to  blocks by the left end and sort all the queries in each block by the right end. Let r be the maximal left end inside the current group then all left ends will be in distance not greater than
blocks by the left end and sort all the queries in each block by the right end. Let r be the maximal left end inside the current group then all left ends will be in distance not greater than  from r and right ends will be in nondecreasing order, so we can move the right end by one (total we will made no more than n movements in each block). During moving of the right end inside some group from the value r + 1 to the value of the current right end we will maintain two tries: the first for the values f(0, x - 1) and the second for the values f(0, x), in the first we will maintain the minimal value of x, in the second — the maximal. After adding some values to the trie we should find the maximal value that can be formed by the current value x. To do that we should go down in the first trie maintaining the invariant that in the current subtree the minimal value is not greater than x. Each time we should go by the bit that is not equal to the corresponding bit in x (if we can do that, otherwise we should go by the other bit). In the second trie we should do the same thing with the difference that we should maintain the invariant that the maximal value in the current subtree is not less than the value x. After moving the right end we should iterate from the left end of the query to r and update the answer (without adding the current value to the tries). Also after that all we should iterate over all the queries and with new empty tries iterate from the left end to r, add the current values to the tries and update the answer.
from r and right ends will be in nondecreasing order, so we can move the right end by one (total we will made no more than n movements in each block). During moving of the right end inside some group from the value r + 1 to the value of the current right end we will maintain two tries: the first for the values f(0, x - 1) and the second for the values f(0, x), in the first we will maintain the minimal value of x, in the second — the maximal. After adding some values to the trie we should find the maximal value that can be formed by the current value x. To do that we should go down in the first trie maintaining the invariant that in the current subtree the minimal value is not greater than x. Each time we should go by the bit that is not equal to the corresponding bit in x (if we can do that, otherwise we should go by the other bit). In the second trie we should do the same thing with the difference that we should maintain the invariant that the maximal value in the current subtree is not less than the value x. After moving the right end we should iterate from the left end of the query to r and update the answer (without adding the current value to the tries). Also after that all we should iterate over all the queries and with new empty tries iterate from the left end to r, add the current values to the tries and update the answer.
С++ solution: in this code the trie number 0 corresponds to the second trie and the trie number 1 corresponds to the first trie.
Complexity: 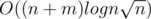 .
.











what about problems E and F ?
E problem can be solved with lazy propagation. The main thing some subtree is represented as list of neighboring elements on dfs list. After that you task is: change elements from interval [L,R] to X, and count how many different elements you have on interval [L,R]. It is clear seg. tree problem and also I think that solution with sqrt decomposition will pass tests.
F problem is pretty hard, if you think about my solution. You can run MO algorithm for queries and after that you can solve task with two tries. Also you should know some performance of xor operation. This solution has complexity O(M sqrt (n) log Ai). Second solution is O(n^2) solution, it is short and interesting. You can read some accepted solution for better understanding that approaches.
For problem E just use the fact that c <=60 then you can make a segment tree where each node contains a bitmask of colours used in this segment and the rest is easy to do.
Done.
Can someone explain E in a better way please ?
I didnt get the part about storing colours as binary bits .
assuming you know how segment tree works, in segment tree: you want to store number of different colors in the range(subtree) covered by a certain node so you can use a bit mask for every node and store that information as following:
for bit_i that represents color_i:
0represents color_i never appeared in the range,1if it appeared one or more times.when updating:
bit-mask_for_node_i = bitmask_of_right_child | bitmask_of_left_childwhen querying: preform binary or
|with all nodes lie in the range you are querying. The answer will be the number of ones in the final mask you get.hope that helps a little bit.
Yeah that helped! Thanks
Is is possible to generalise the problem D for any k?
I don't beleive in it. I was thinking about such option during preparation, but I didn't manage to solve it. Maybe some red coder can help with it ;)
At least it is definitely going to be very hard for large values of k.
Let's take first array with sum S and second array consisting of 0's only. Now it turns out that we want to pick subset of first array and move it to second array in such a way that sum of this subset is as close to S/2 as possible. In case k>=n/2 you have to solve knapsack problem :)
This is good solution for k>=n/2, but I am interested how would you save informations about swaps ? I think that is only possible in cases with really small Ai.
I must think about some harder problems in next period, now I don't have them for next round :D
Complexity will grow for bigger k. nC1+nC2+nC3+...+nCk is the general complexity, AFAIK.
Problem F is really interesting and I think it's a mixture of these two : 86D - Powerful array (MO Algorithm)
282E - Sausage Maximization
Nice :)
Who can tell me why I got TLE on #64, the last test case, in problem E? I have tried so many ways to solve it but they all didn't work... It's just so strange...
I am getting timeout error for problem C. Please Refer this to view my code. I am not able to find the possible solution to this. Please if anyone can indicate what's wrong!
Change temp from vector to set.
Also, check your solution again as it doen't even give correct answer for the sample test case. It gives -1 instead of
1
1 5
I run my code on ideone.com but it gave -1. I run the same code on codeforces custom test section, it gave correct ans. I don't know what caused the error on ideone! And I got timeout error on test case 32 even when I used set instead of vector for temp! Can you suggest any other modifications?
http://www.cplusplus.com/reference/algorithm/find/
http://www.cplusplus.com/reference/set/set/find
Can you see the difference? First algorithm doesn't know what's under the hood (is it vector or set) so it has to go through elements one by one. Second one can use knowledge about the structure to optimize findings and therefore reduce complexity from linear to logarithmic ("default" complexity for search in a set).
Can anyone give me any ideas why this solution is getting TLE:http://mirror.codeforces.com/contest/620/submission/17684134? It's pretty much the same idea as listed in the editorial but implemented with set instead of map.
Why is inserting / lower_bound on a set much slower than it is in a map in this particular case?
Can someone explain the logic behind this code for F written by waterfalls
15602452
please tell me anyone, why my soltuion of problem E is give wrong output in first code but it give correct answer in second code (https://mirror.codeforces.com/contest/620/my)
You have to also take care of long long,check all 61 bits. I was doing the same mistake.