Только что закончился Гран-При Азии. Подскажите, как решать задачи B, J ?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
40:37:17
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
40:37:17
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 00:57:44 (h2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










J: Если выполняется условие, что сумма степеней 2n-2 , то ответ это вторая формула в http://e-maxx.ru/algo/prufer_code_cayley_formula#9
The intended solution doesn't require any theorem.
Let x, y, z be the number of vertices with degree 1, 2, 3, and let f(x, y, z) be the answer.
1) If y > 0, f(x, y, z) = f(x, y-1, z) * (the number of edges), because we can "insert" a vertex of degree 2 in the middle of an edge. 2) If y = 0, except for some small cases, f(x, y, z) = f(x-1, y+1, z-1) because the removal of one particular leaf will change a vertex of degree 3 to a vertex of degree 2.
z always equals to x-2, otherwise answer is 0
ans(x,y)=y*ans(x,y-1)+(x-2)*ans(x-1,y+1);
Как решать А и Н?
Quick hints:
A: We can generate all divisorful numbers. If we consider only 3-smooth numbers and define divisorful numbers similarly, can you compute all such numbers? How about 5-smooth numbers? 7-smooth numbers? And so on.
H: First, for each i, compute the number of ways such that
Start from (0, 0).
Walk for i steps.
After i steps, return to the original position for the first time.
too quick hint for H :) Could you tell a little bit more about last step in your solution?
The number of visited cells is (N + 1) — duplicates.
Then, duplicates can be counted as the number of pairs (p, q), such that the positions at time p and time q are the same, and this position is never visited between p and q. Here the result from the first step (with i=q-p) can be applied.
Can you please explain A/H in english?
H: Сначала нужно перейти от мат. ожидания к сумме по всем клеткам вероятности, что мы когда-либо окажемся в этой клетке. Теперь рассмотрим любую клетку на некотором пути. Пусть в последний раз на этом пути мы оказались в ней после k-го шага. Тогда нам нужно прибавить к ответу вероятность того, что мы придём в клетку (x, y) на k-м шагу и после этого больше не вернёмся в эту клетку за оставшиеся n - k шагов. Обозначим zk — количество способов выйти из (0, 0), сделать k шагов и ни разу не вернуться в (0, 0).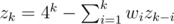 , где
, где 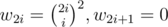 — количество способов попасть в (0, 0) за i шагов, стартовав из (0, 0). Таким образом, ответ это
— количество способов попасть в (0, 0) за i шагов, стартовав из (0, 0). Таким образом, ответ это 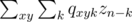 , где qxyk — количество способов попасть в (x, y) из (0, 0) за k шагов. Если поменять порядок суммирования, то qxyk просуммируется к 4k. Таким образом, ответ это просто
, где qxyk — количество способов попасть в (x, y) из (0, 0) за k шагов. Если поменять порядок суммирования, то qxyk просуммируется к 4k. Таким образом, ответ это просто 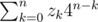 .
.
B: Найдем 4 точки (max(x+y), min(x+y), max(x-y), min(x-y)). Добавим все ребра, концами которого есть хотя бы одна из этих точек. Найдем максимальное остовное дерево в таком графе. Минимальное взятое ребро и будет ответом.
а можно доказательство этого решения
Пусть в ответе есть ребро (x1,y1)--(x2,y2), и для определённости x1<x2, y1<y2. Пусть точка (x4,y4) — это максимум x+y, а точка (x3,y3) — это минимум x+y. Тогда следующие три ребра не короче нашего: (x1,y1)--(x4,y4)--(x3,y3)--(x2,y2), и поэтому наше ребро не нужно.
Другое решение — поменяем координаты точек на (x[i]+y[i],y[i]-x[i]). В таких координатах манхеттенское расстояние равно максимуму модулей разностей координат.
Переберем ответ двоичным поиском и будем явно строить граф.
Две вершины будут связаны, если модуль разницы хотя бы по одной из координат не меньше текущего ответа.
Посмотрим все точки в порядке сортировки по первой новой координате. Первая в порядке сортировки точка будет соединена с каким-то суффиксом такого массива, последняя — с каким-то префиксом. Очевидно, что других важных ребер нет. Аналогично проведем нужные ребра по второй координате.
Получившийся граф проверим на связность и в результате куда-то сдвинем границу бинпоиска.
У вас тоже не работали сервера Div.2 в последний час?
How to solve M?
When N is odd, put N points around a circle, and choose all isosceles triangles.
When N is even,
Put N-1 points around a circle, and choose all isosceles triangles.
Add (the remaining point) — (i) — ((i+1)%N) for each 0 <= i < N.
Add (the remaining point) — (i) — ((i+2)%N) for each 0 <= i < N.
Remove extra triangles.
We should find proper coefficients but basically this is the idea of the answer.
Seems that you mixed up odd and even
What does equal number of trianges in your solution for odd and for even n?
If you are interested in details, here is my solution: http://ideone.com/o9GMsI
Got it.
Еще интересно решение по С.
Сгенерить все разности, и понять, куда мы можем сдвинуться за четное число ходов — это все возможные суммы этих разностей. Можно доказать, что если мы хотим попасть в что-то в пределах 10^4, то можно за эти пределы не выходить, поэтому bfs работает за 104 * 104
Можно проще: заметим что каждый нечетный ход добавляется к позиции, а четный отнимается. Тогда мы будем делать bfs на таком графе: каждой позиции на линии соответствуют две вершины, одна — это минимальное расстояние при условии что последний ход был нечетным, вторая соответственное что четным. Это будет n * 2 * 10 ^ 4
What is test #3 in problem L ?
My team had the same problem. We mistakenly believed that the line of "e" can not get the string "egg". After fixing, we passed the test. Perhaps a similar case in the test 3. P.S. Sorry for my bad english
How to solve G?
Див. 2: Примерно с 4-ого часа соревнований — "Service is not available". До сих пор.
уже все в порядке, но contest is over
How to solve F?
Few corner cases. If we have only one color, the answer is -1. Another corner case is the second sample — we have some cards of the same color and a card of some other color between them. The answer is 0 in this case.
Now let's move to the general approach.
Let's decrease each a[i] by one. Now we have to find the amount of such numbers k, the a[i]/k == a[j]/k if and only if c[i] == c[j].
The key observation is that for fixed number N there are only different values of N/i for all possible values of i.
different values of N/i for all possible values of i.
Based on this we can build a set of constraints in form of
1) Segment [l; r] may be the answer (we get this from a pair of cards with the same color)
2) Segment [l; r] can not in be the answer (we get this from a pair of cards with different colors)
To find the answer we should find the total length of the segments, that are covered by all of the constraints of the first type and are not covered by any of the segments of the second type. This can be done using some kind of a sweeping line.
Code
By the way, you asked the question in the Russian thread
Thanks. In English thread most comments aren't visible. So i switched to russian thread. But when posting the comment i forgot to post it in English thread.
Where can I find the final standings?
Division 1
Division 2
how to solve I?
We only need some edges. For every point we can reach this point from maximum 4 points(point J which has smallest Y, X[I] = X[J] and Y[J] > Y[I] and have direction 'D'.also for all other 3 direction). So we only have maximum 4 * N edges and now we can use simple dijkstra algorithm to get switch time of every robot. solution author LashaBukhnikashvili
How to solve D?
If someone is still interested in solution, it's dp[i][j] where i and j are the suffixes of the given permutations. If s1(i) != s2(j) then dp[i][j] = dp[i + 1][j] + dp[i][j + 1]. If s1(i) = s2(j) so let len be the length of the longest common prefix of these suffixes. Then we are in danger of counting some array twice untill one of our indices(i or j) has reached position i + len + 1. So let's say i will move to i + len + 1 before j will move to j + len + 1. Let's try every k so that we will go to the state dp[i + len + 1][len + k], k <= len. We need to count number of arrays that can be obtained from substring (i ... i + len) of the first permutation and from substring (j ... j + k — 1) of the second permutation. We will avoid double counting if we will not take number from the second permutation if we took less numbers from the first permutation. So it's equivalent to the number of bracket sequences with len opening brackets and k closing brackets. It can be precomputed by simple dp or using formula described in this comment http://mirror.codeforces.com/blog/entry/23266?#comment-276645. Then we have do the same for the index j. There are only O(n) such states.
Does anyone know how to solve problem J?
Pleade read about Prufer codes (that's a bit overkill, but a very nice one).