Уважаемые форумчане! Подскажите, пожалуйста, в каком направлении "копать" следующую задачу. Идей нет. Написать программу, которая пытается найти оптимальную раскраску для заданного графа. Цвета применяются к вершинам графа и доступны только два цвета: черный и белый. Раскраска графа называется оптимальной, если в ней максимальное количество чёрных вершин. Раскраска ограничена тем правилом, что не может быть двух смежных чёрных вершин. Спасибо.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:52:52
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:52:52
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 15:42:09 (l3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Эта задача называется "максимальное независимое множество" и является NP-полной. Так что нужно думать в сторону какого-то перебора.
Тут ведь только два цвета. Достаточно правильно раскрасить двудольный граф за O(N). И цвет, который встречается больше раз, сделать черным.
Две былых вершины могут быть смежными.
Действительно. Не заметил. Благодарю
Я так делал. Это не верное решение. Вот например есть одна вершина и из нее выходит 5 , а потом все 5 сходятся в одну. Здесь выгодно первую сделать белой все 5 черными, а последнюю белой.
Твой пример не ломает решение, а этот ломает.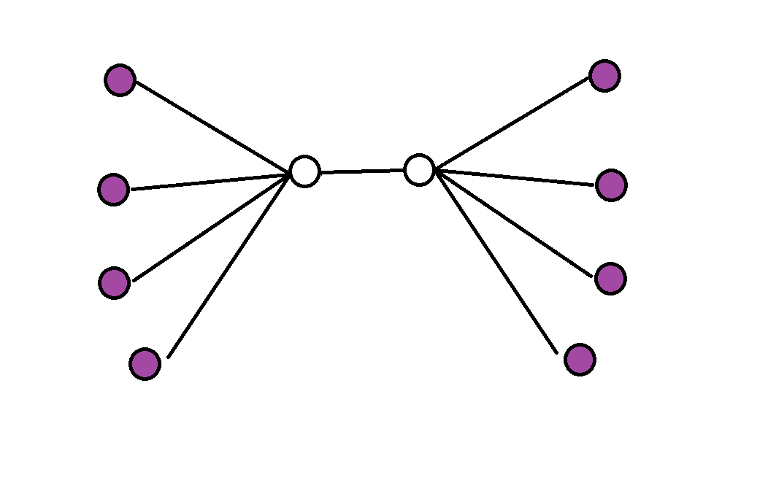
Согласен. А если всегда начинать с вершин с наибольшей степенью и смежные раскрашивать в черный цвет.
Сдал эту задачу на e-olimp, но решение не очень хорошее. Если интересно — могу рассказать.
А задача из жизни или с контеста? В смысле, тесты случайные или "умные"? Может, стоит загнать что-нибудь рандомизированное? Например(в качестве первого пришедшего в голову решения) перебирать вершины в случайном порядке, если очередная вершина еще не запрещена — добавлять в "черные" и запрещать все смежные с ней?
P.S. разумеется, такое нужно запустить несколько раз, наилучший ответ выводить