It will be fully translated later, sorry for slowpoking :(
Blackjack (problem A, div-2). The problem's author is Alex_KPR | ||
| Obviously, suits are not change the answer. Look at all possible situations: [0 - 10] — zero ways. | |
| Complexity is O(1). |
| Testing Pants for Sadness (problem B, div-2; problem A, div-1). The problem's author is Alex_KPR | |
| We can't move to the i + 1-th question before clicking all answers at i-th question. We will move to the very beginning clicking at ai - 1 answers and only one will move us to the next step. Every way from beginning to i-th question have length equal to i - 1 plus one for click. There is a simple formula for i + 1-th question: ci = (ai - 1)· i + 1, 1-based numeration. Let's summarize all values of ci for making the answer. | |
| Complexity is O(n). |
| Cthulhu (problem C, div-2; problem B, div-1). The problem's author is Alex_KPR | |
| Look at the formal part of statement. Cthulhu is a simple cycle with length of 3 or more and every vertix of the cycle should be a root of some tree. Notice this two important facts: a) Cthulhu is a connected graph If we add only one edge to tree (not a multiedge nor loop) then we will get a graph that a) and b) properties. There is a simple solution: let's check graph for connectivity (we can do it by one DFS only) and check n = m restriction. If all are ok then graph is Cthulhu. | |
Complexity is O(m). |
| Russian Roulette (problem D, div-2; problem C, div-1). The problem's author is Alex_KPR | |
| Let's solve the problem when value n is even. Obviously, if k = 1 we should put a bullet at most right position. For example, choose n = 8 and our answer string will be: .......X Let's find probability of winning at this situation. We will write zeros at losing positions and ones at winning positions: 10101010 The simple idea is to put every next bullet for non-dropping down our winning chance as long as we can. After that we should put bullets in lexicographically order with growing value of k. Look for the answer for another k's with n = 8: .....X.X When n is odd our reasoning will be the same with a little bit difference at the beginning. Look at the answer with n = 9 and k = 1:: ........X We may put second bullet as at even case. But there is exists another way, we may put our bullet at 1st position and turn left the cylinder, look here: X.......X => .......XX Obvioulsy probability of winning was not changed but answer made better. Next steps of putting are equal to even case: .....X.XX There is no difficulties to give answers to queries. | |
Complexity is O(p). |
| Time to Raid Cowavans (problem E, div-2; problem D, div-1). The problem's author is Alex_KPR | |
| Let's solve this problem by offline. Read all queries and sort them by increasing b. After that there are many effective solutions but I tell you a most simple of them. Look at two following algorithms: 1. For each (a, b)-query calculate the answer by the simple way: for(int i = a; i < n; i += b) 2. Fix the value of b and calculate DP for all possible values of a: for(int i = n - 1; i >= 0; i--) Obvioulsy, the 1st algorithm is non-effective with little values of b and the 2nd algorithm is non-effecitve with very different values of b. Behold that it's impossible to generate the situation where all b's are so little and different simultaniously. There is a simple idea: we may solve the problem by 1st algo if values of b are so large (if they are greater than c) and solve by 2nd algo if values of b are so small (if they are less of equal to c). We need to sort our queries because of no reason to calculate DP of any b more than once. If we choose c equal to |
|
Complexity is |
| Buying Sets (problem E, div-1). The problem's author is winger | |
| Translated by Borisp. |
|



 that we will get a
that we will get a 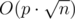 complexity.
complexity.







Can anyone explain why the complexity for Time to Raid Cowavans (Div1-D) is O(P * sqrt(N))? I'm new to this complexity analysis stuff
Because we use 1-st method only for queries where
B >= sqrt(N), so each query runs inO(sqrt(N))time. 2-nd method worksO(n)time for initializing arrayd, andO(1)to answer each query. We don't need more thansqrt(N)initializations, because we use 2-nd method only for groups of queries whereB < sqrt(N). Total complexity isO(sqrt(N) * p1 + sqrt(N) * N + p2) = O(sqrt(N) * max(N, P)).p1— number of queries whereB >= sqrt(N), andp2 == p - p1.Thanks for the detailed explanation!
Exactly, so there is a mistake in the solution where they say the complexity is O(sqrt(n) * p). It's actually O(sqrt(n) * max(n, p).