Div 2. Задача А. Cifera
Если переформулировать задачу то необходимо было определить является ли число l, некоторой положительной степенью числа k. Для этого можно делать одно из двух:
1) В 64-битном типе данных найти минимальную степень h числа k, такую что kh ≥ l. Если kh = l, то ответ YES, и число артиклей - h - 1, иначе NO.
2) Будем делить l на k, пока l делится на k и l ≠ 1. Если l = 1, то ответ - YES и число делений-1, иначе ответ NO.
Div 2. Задача B. PFAST Inc.
Задачу можно понимать следующим образом:
Дан граф, необходимо найти в нем клику наибольшего размера. Если взглянуть на ограничения n ≤ 16, то можно понять, что искомое подмножество вершин можно просто перебрать. Что мы и сделаем. Для удобства перебора можно воспользоваться бит. масками и просто перебрать до 216 чисел проверяя получаемый граф на то является ли он кликой. Единственное что остается - не забыть отсортировать имена при вводе.
Div 1. Задача A. Grammar Lessons
Данная задача скорее на аккуратную реализацию.
Половиной решения задачи является внимательное чтение условия. А именно - необходимо проверить набор слов который нам дается, на то — является ли он предложением в заданном нам языке. По условию корректным предложением является - 1 слово из нашей грамматики или же структура вида:
{ноль или несколько прилагательных} существительное {ноль или несколько глаголов}
Собственно авторское решение делало следующее:
Считаем все слова - если оно одно, то проверяем относится ли он к грамматике, иначе узнаем из первого слова - род. А дальше идем по всем словам проверяя, чтобы было согласование рода, наличие ровно 1 существительного, а также соблюдения порядка данного в условии.
Div 1. Задача B. Petr#
Данная задача имеет несколько решений. Начну с самого простого (правда которое с некоторой вероятностью можно взломать).
Первое решение. Посчитаем хеш-функцию от нашей строки. Тогда мы получаем возможность сравнивать подстроки за O(1). Далее пройдемся по всем позициям строки и найдем те в которых может начинаться begin, после чего для данной позиции найдем все подходящие позиции end которые подходят для данного begin, используя сравнение строк через хеши, после чего посчитаем число различных значений хеш-функции которые мы смогли получить (можно например используя массив для запоминания полученных хешей и сортировкой оного). Сложность - O(N2 Log N). Однако можно сделать более аккуратно, уменьшив вероятность коллизий. Для этого сначала найдем все возможные позиции начал, а после этого будем перебирать длину искомой подстроки и считать число уникальных хешей данной длины. Заметим что при этом мы все равно каждую подстроку переберем ровно 1 раз, однако коллизии будут возможно только между строками одной длинны, что менее вероятно, чем когда мы рассматриваем все строки.
Второе решение. В лоб найдем все возможные позиции начал и концов. После чего отобразим данную строку в число 0. После этого будем добавлять по 1 символу к имеющимся строкам и перенумеровывать строки данной длинны, т.е. уже строить для строк длины на 1 больше опять же отображения в целые неотрицательные числа. Заметим, что при этом у нас не будет никогда возникать более чем 2000 различных строк, поэтому мы их сможем спокойно перенумеровывать. Теперь учитывая, что мы знаем все концы строк, и различным строкам одной длины соответствуют разные числа, а одинаковым одинаковые, то мы без труда можем посчитать число различных подстрок указанной длины точно. Касательно сложности - O(N2 Log N), в силу того что всего у нас N итераций каждая из которых выполняется за время O(N Log N).
Третье решение. Используя суффиксный массив данную задачу можно решить за время O(N Log N). Построим суффиксный массив с LCP за O(N Log N). Далее найдем все вхождения строки end в нашу строку и запомним эти вхождения в отсортированном порядке в некотором массиве. Будем рассматривать последовательно наши суффиксы которые начинаются со строки begin (первое и последнее вхождение ищутся достаточно просто). Для начала рассмотрим первый суффикс который начинается с со строки begin. Для него любая строка закачивающаяся на end и такая что её длина больше чем max(|begin|, |end|) является искомой подстрокой, причем найти такую позицию строки end мы можем используя дихотомию по заранее посчитанному массиву вхождений концов (и тогда очевидным образом получаем сколько строк нам подходят). Рассмотрим следующий суффикс. Заметим что для следующего суффикса любая строка которая которая закачивается на расстоянии не больше чем LCP(i, i - 1) от начала строки (где i номер текущего суффикса), будет совпадать с некоторой подстрокой предыдущего суффикса, т.е. её мы посчитали. А любая строка заканчивающаяся после LCP(i, i - 1) (где i номер текущего суффикса) будет лексикографически больше любой рассмотренной ранее подстроки, а значит любое такое вхождение — новая подстрока. Используя дихотомию найдем в массиве концов - первый подходящий. Таким образом мы посчитали число различных подстрок в данных двух суффиксах. Продолжим делать таким образом пока не рассмотрим все суффиксы начинающиеся со строки begin. Таким образом мы получили ответ.
Теперь оценим сложность. На построение суффиксного массива мы потратили время O(N Log N). Построение массива концов - делается за O(N). Всего начал - не более чем N и при этом на каждой итерации мы тратим время O(Log N). Т.е. итоговая сложность O(N Log N).
Div. 1. Задача C. Double Happiness
В задаче необходимо было найти число простых чисел представимых в виде суммы двух квадратов натуральных чисел. Очевидно, что простые вида 4k + 3, не подходят, т.к. сумма двух квадратов не может быть сравнима с 3 по модулю 4. Что же касается простых вида 4k + 1, то можно доказать (ну а вообще это достаточно известный факт), что любое просто такого вида представимо в виде суммы двух квадратов натуральных чисел. Также необходимо не забыть про 2. Теперь касательно того как всё это можно сдать в систему. Очевидно, что совсем тупо писать решето Эратосфена не проходит по памяти, однако можно использовать блочное решето Эратосфена, которое работает за те же O(N Log Log N), однако использует в разы меньше памяти например 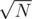 . Помимо этого можно было использовать препросчет, и сократить объем работы до куска который влазит в память. Также участник Romka воспользовался идеей, что можно используя bit-mask уменьшить объем необходимой памяти для всего решета в 8 раз, что отлично влезло в ML. Так же неплохо при написании решета рассматривать, только нечетные числа.
. Помимо этого можно было использовать препросчет, и сократить объем работы до куска который влазит в память. Также участник Romka воспользовался идеей, что можно используя bit-mask уменьшить объем необходимой памяти для всего решета в 8 раз, что отлично влезло в ML. Так же неплохо при написании решета рассматривать, только нечетные числа.
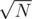 . Помимо этого можно было использовать препросчет, и сократить объем работы до куска который влазит в память. Также участник Romka воспользовался идеей, что можно используя bit-mask уменьшить объем необходимой памяти для всего решета в 8 раз, что отлично влезло в ML. Так же неплохо при написании решета рассматривать, только нечетные числа.
. Помимо этого можно было использовать препросчет, и сократить объем работы до куска который влазит в память. Также участник Romka воспользовался идеей, что можно используя bit-mask уменьшить объем необходимой памяти для всего решета в 8 раз, что отлично влезло в ML. Так же неплохо при написании решета рассматривать, только нечетные числа.Div. 1. Задача D. Museum
Для начала избавимся от того что у нас есть 2 человека, каждый из которых переходит в некоторую вершину. Для этого сделаем состоянием пару чисел (i, j) - которая обозначает, что Петя находится в комнате с номером i, а Вася в комнате с номером j. Тогда встрече в комнате i будет соответствовать состояние (i, i). Тогда исходя из этих данных несложно построить матрицу переходов - т.е. матрицу в которой для каждого состояния (i, j), известна вероятность перехода в состояние (x, y), где 1 ≤ i, j, x, y ≤ n. Так же понятно, что из состояния встречи мы переходим в это же состояние.
Теперь рассмотрим как решить данную задачу. Если бы нам было необходимо просто посчитать вероятность встречи в первой комнате, то можно было бы сделать следующим образом: построим систему линейных алгебраических уравнений:
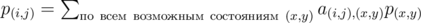 , где a(i, j), (x, y) — вероятность перехода из состояния (i,j) в состояние (x,y). При этом p(1, 1) = 1, а p(i, i) = 0 при i ≠ 1. При этом нас интересует p(a, b).
, где a(i, j), (x, y) — вероятность перехода из состояния (i,j) в состояние (x,y). При этом p(1, 1) = 1, а p(i, i) = 0 при i ≠ 1. При этом нас интересует p(a, b).Данная СЛАУ легко решается методом Гаусса. Аналогичным образом можно решить для оставшихся вершин, однако при этом сложность выходит O(n7), что при данных ограничениях нас не очень устраивает. Однако можно заметить, что мы каждый раз решаем одну и ту же СЛАУ Ax = b (при условии, что у нас в матрице , единственное что меняется — вектор b), поэтому можно построить LU-разложение и пользуясь им получить сложность O(n6), однако можно не строить LU-разложения, просто решать матричное уравнение где b - матрица размерности n2 * n, а ответом является значение получившееся в строке соответствующей состоянию (a, b). При этом нетрудно видеть, что сложность получается опять же O(n6). Кроме этого можно решить задачу просто выразив все состояния через переменные соответствующие состояниям встреч.
Div. 1. Задача E. Sleeping
Введем функцию F(x) (где x - некоторый момент времени) — число моментов времени от 00..00:00..00 до x (т.е. x не переключается на следующий момент времени) когда сменится не менее чем k цифр. Тогда интересующим нас ответом будет являться F(h2: m2) - F(h1: m1), при этом мы учитываем что если h2: m2 < h1: m1, то F(h2: m2) будет на сутки больше.
Теперь научимся считать функцию F(x). Для начала посчитаем сколько наступит таких моментов без смены часа. Т.к. час у нас не меняется, то значит в минуте у нас должно поменяться не менее чем k цифр, но для того чтобы в числе поменялось не менее чем k цифр, необходимо, что наше число имело вид:
a..a99...9, где a - произвольные цифры, а на конце - k-1 девятка. Т.е. k цифр меняются каждое число кратное 10k - 1.
А значит в моменты в которые не меняется час у нас случилось таких событий 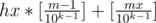 , где hx и mx - число часов и минут в момент времени x, а [] - целая часть.
, где hx и mx - число часов и минут в момент времени x, а [] - целая часть.
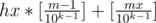 , где hx и mx - число часов и минут в момент времени x, а [] - целая часть.
, где hx и mx - число часов и минут в момент времени x, а [] - целая часть.Теперь рассмотрим моменты когда меняется час. Если меняется час значит минут переходят из m - 1 в 0, и поэтому у нас уже отличается y цифр, где y - число не нулевых цифр числа m - 1. Значит нам надо аналогичным образом посчитать для часов, число моментов когда изменится не менее чем k - y цифр. k - y цифр меняется каждое число кратное 10max(0, k - y - 1), т.е. таких моментов — 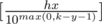 . Т.е.
. Т.е. 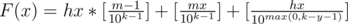 .
.
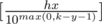 . Т.е.
. Т.е. 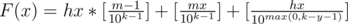 .
.Если, что-то плохо описано или содержит опечатку/ошибку, отпишитесь в коментариях - исправлю.











Upd: Прошло. Жаль, что не увидел во время контеста, что может быть такая ситуация
is it possible to solve it greedy ??!
i mean ..
1.clear the person that doesn't get on well with the max number of people
if there still some one doesn't get on well with another
repeat 1
else
print the ans
__
is that okay?!
in your case b is the person that doesn't get on well with the max number of people (a and c)
then first remove b
that gives a and c with no problems
then the ans is 2 a c
5 4
a
b
c
d
e
a d
a e
b d
c e
----
the answer is 3 a, b, c . but it's not achievable using greedy.
and connect every pair of vertices that are diametrically opposed.
The biggest clique is of size two, and all degrees are 3.
Add a triangle.
The biggest clique is now the triangle, but the first three vertices removed would be those of the triangle.
update: Here is a corresponding testcase. The answer is "g h i".
9 24
a
b
c
d
e
f
g
h
i
a c
a e
c e
b d
b f
d f
a g
a h
a i
b g
b h
b i
c g
c h
c i
d g
d h
d i
e g
e h
e i
f g
f h
f i
Anyone has a reference for an explanation of this algorithm?
choosing from between them randomly ...(first to find or last , depends on ur Algorithm) won't give the right answer for all the cases ...
Так просто достаточно удобно перебрать все подмножества (хотя и обычный DFS тоже подходит).
Перенумеруем всех людей числами от 0 до n-1 (всего n людей). И будем рассматривать числа из n бит, при этом если i-ый бит равен 1, то берем соотсвествующего человека, иначе нет. Тогда если мы рассмотрим все числа от 0 до 2n - 1, то мы переберем все возможные подмножества из данного множества. А зная каких людей мы берем легко проверить, что все ли они не конфликтуют.
Suffix tree/array seems to be most efficient way to solve B.
Thanks. good editorial
In problem E, the formula of $$$F(x)$$$ should be
Yes, there is some problem with border processing.
can anybody provide code for Div 1. Problem B. Petr# using editorial approach. i'm getting MLE :(
:) can u help me pls, i got wa on test 24
I looked at your submission but couldn't understand it (sorry!) but i can tell you what i did.
I simply store all indices (start) of s which begin with s_beg and all indices (end) that end with s_end. then for each pair of start,end i store hash of substring to ensure no substring is counted more than once. 222393498
I hope it helps :)
thanks