ikk's blog

Upper bound of the running time of the bipartite matching algorithm
By ikk, 13 years ago, In English

Some resources found on the Web state that the running time of the bipartite matching algorithm (as found in UL: Undefined's solution) is O(|V|(|V| + |E|)).  I suspect, however, that there exists a better upper bound for this.  In Problem H of Saratov Regional, the number of the vertices can be as large as 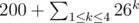.  A Θ(|V|(|V| + |E|)) algorithm usually gives TLE for graphs of this size, but many participants got ACs by submitting that algorithm.

I suspect the running time is determined by the lesser of the number of vertices on the left and the number of vertices on the right.  Am I wrong?  I couldn't prove or disprove myself.

  • Vote: I like it
  • +4
  • Vote: I do not like it

13 years ago, # |
  Vote: I like it +1 Vote: I do not like it
you can read about time here, but it's in russian (google translate ;))
→ Reply
  • 13 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Thanks.  (It seems I should forget Latin to make room for Russian...)  I didn't know  the algorithm has a name at all.

    → Reply
13 years ago, # |
  Vote: I like it 0 Vote: I do not like it
This algo is the best for bipartite graphs
→ Reply
13 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Yes, the running time is O(X (|V|+|E|)), where X is the number of vertices on the left. So if we choose left side as smaller side and right side as larger - it will be much faster that vice versa.

Also it's widely known that in reality this upper bound is never reached.

Additionally, there exists a trick, when before executing the DFS you try to find an straight edge to a non-saturated vertex. This trick greatly improves the running time, and makes the algorithm applicable even for thousands of vertices.

→ Reply
  • 13 years ago, # ^ |
    ← Rev. 3   Vote: I like it +1 Vote: I do not like it

    more precisely, Kuhn is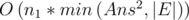 , where n1 is a size of left side, and Ans is the result.

    → Reply
    • 13 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it
      Thanks.  Could you please tell me how to prove it?
      → Reply
      • 13 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it
        Consider one Kuhn's run. For the current Ans, DFS will not visit more than Ans2 edges (it stops because of path found or all matched vertexes visited). There will be no more than n1 runs.
        → Reply
        • 13 years ago, # ^ |
          ← Rev. 3   Vote: I like it 0 Vote: I do not like it

          Another question is whether this algorithm is called Kuhn's in the literature.  After a bit of Googling it seems Kuhn's algorithm usually refers to the one based on matrices.

          → Reply