Задача A.

Задача решается с помощью поиска максимального потока. Проведём ребра от истока ко всем ядрам, от ядер к пушкам, если мы успеем взять его и принести обратно, от пушек к целям, если пушка в состоянии достать до неё, и от всех целей до истока. Все рёбра имеют пропускную способность 1. И надо ещё заметить, что, так как пушка может стрелять только 1 раз, то вершины, отвечающие за пушки надо раздвоить.

Задача B.

Не знаю, как можно решить её по-нормальному, но я сдал её рандомом. Пометим случайно все рёбра числами от 1 до 3 * n. Далее 20 000 раз проделаем следующую операцию: за 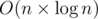определим есть ли две тройки с одинаковой суммой, если есть, тогда выберем случайное число из первой тройки и случайное число из второй тройки и поменяем их местами. Так как числа разные, то суммы у этих троек теперь станут разными.

Задача C.

Сначала избавимся от игры на круге и перейдём к игре на ленте, для этого просто будем считать, что первый игрок сделал какой-нибудь ход, не важно какой, так как все они приведут к ленте размера n - 3. Далее, заметим, что после хода мы можем получить либо эту же игру меньшей размерности, либо сумму игр. Поэтому для решения задачи надо для каждой позиции посчитать значения функции Гранди.

Задача D.

Определим функцию Count:

int Count(int n, int k) {return n / k;}

Тогда количество чисел на отрезке [l, r], которые делятся на k будет равно Count(r, k) - Count(l - 1, k).

Пусть ответ больше двух. Покажем, что тогда все числа будут иметь одинаковый остаток при делении на k. Возьмём любые три числа a, b и c, тогда:

a + b ≡ 0(mod k)
b + c ≡ 0(mod k)
a + c ≡ 0(mod k)

Вычтем из первого сравнения второе, получим:

b - с ≡ 0(mod k)
b ≡ c(mod k)

Аналогичным образом получим, что a ≡ b(mod k). И следовательно a ≡ b ≡ c(mod k).

Поэтому если ответ 3 или больше, то достаточно найти количество чисел на отрезке [l, r], которые делятся на k. Для случая нечётного k этого достаточно, а если k чётно, то надо ещё посчитать количество чисел на отрезке, которые дают остаток k / 2 при делении на k:

Count(r + k/2, k) - Count(l - 1 + k/2, k)

Теперь рассмотрим случай, когда ответ 2. Нам надо определить, есть ли 2 различных числа на отрезке которые в сумме дадут число, делящиеся на k. Проверим 2 пары (l, l + 1) и (r - 1, r). Если ни одна из них не подошла, то проверим неравенство

(l + (l + 1)) / k < ((r - 1) + r) / k

Если оно верно, то это значит, что на отрезке найдутся 2 подходящих числа, иначе нет такой пары. Покажем, что это 2 различных числа. Обозначим эти числа за a и b. Если они равны, то они не могут равняться ни l, ни r. И вместо них можно взять числа a - 1 и b + 1, сумма которых тоже будет делится на k, и они будут принадлежать нашему отрезку.

Задача E.

Даны два массива целых чисел A и B, требовалось поксорить i-й элемент массива A с i-м элементов
массива B.

Задача F.

Вероятность попадания равна s / S, где s - площадь многоугольника, S - площадь круга. Посчитаем вероятность попасть ровно i раз. Для этого надо взять вероятность того, что мы попали i раз, умножить на вероятность промахнуться 30 - i раз, и умножить на количество вариантов попасть и промахнуться. Итого, ответ получается:

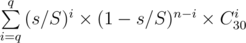
Задача G.

Посчитаем за O(n) хеши всех циклических сдвигов заданной строки и добавим их в сет. Теперь нас будет интересовать только хеш текущей строки. После замены двух символов пересчитываем за O(1) хеш, и проверяем, не совпал ли он с каким-нибудь хешем из сета.

В первой посылке я сделал основание 30 и получил WA 13, изменил на 31 и прошло.

Задача H.

Ответ на задачу: 4 * (n / 3) + n\%3

Задача I.

Зафиксируем начальную точку p₁ - середина какой-нибудь стороны, например AB. 
На других сторонах возьмём точки p₂ и p₃ так, чтобы расстояние r до точки C было одинаковое. За p₄ обозначим холм. Рассмотрим путь p₁ -  > p₂ -  > p₄ -  > p₃ -  > p₁. Заметим, что его длина является унимодальной функцией относительно r. Найдём r тернарным поиском и посчитаем длину пути.
Почему этот путь оптимальный я доказать не могу.