Пока участники Codeforces развлекались, выясняя, кто из них самый аутентичный JKeeJle30, David Eppstein подвел итоги ушедшего года в области Computer Science. Изучив появившиеся за этот год препринты на arxiv.org в разделе cs.DS (да, поэтому результаты про перемножение матриц сюда не попали) он выбрал десятку самых понравившихся ему. Вот они, в хронологическом порядке:



Solving connectivity problems parameterized by treewidth in single exponential time. В первую очередь обращает на себя список авторов - Marek Cygan, Jesper Nederlof, Marcin Pilipczuk, Michał Pilipczuk, Johan van Rooij, and Jakub Onufry Wojtaszczyk. Немного о терминологии: декомпозиция дерева - это отображение графа на дерево, когда каждая вершина графа отображается на некоторое поддерево, причем если вершины были смежными в графе, то в дереве есть как минимум одна вершина, которая содержит обе исходные. Treewidth (не рискну переводить на русский) - это ширина минимальной такой декомпозиции. Подробнее о терминах. В 1984 году было показано, что treewidth является хорошей мерой сложности для различных NP сложных задач на графах. Полученный результат:
Существует алгоритм, основанный на методе Монте-Карло, который при заданной декомпозиции графа при ширине t решать следующие задачи:
- STEINER TREE, FEEDBACK VERTEX SET, CONNECTED VERTEX COVER - за 3^t|V|^O(1)

-CONNECTED DOMINATING SET, CONNECTED FEEDBACK VERTEX SET, CONNECTED ODD CYCLE TRANSVERSAL, MAXIMUM FULL DEGREE SPANNING TREE и GRAPH METRIC TRAVELLING SALESMAN PROBLEM (для ненаправленных графов) - за 4^t|V|^O(1)

-MIN CYCLE COVER, LONGEST PATH, LONGEST CYCLE - за 4^t|V|^O(1) для ненаправленных графов и за 6^t|V|^O(1) для направленных графов.

-EXACT k-LEAF SPANNING TREE - за 4^t|V|^O(1) для ненаправленных графов

-EXACT k-LEAF OUTBRANCHING - за 6^t|V|^O(1) для направленных графов

Эти алгоритмы не могут давать ложных положительных результатов, а ложные отрицательные - с вероятностью не более 1/2.

Кроме того, для некоторых случаев было показано, что если константы, встречающиеся во временных оценках удастся улучшить это будет означать ложность утверждения P != NP

3-SAT faster and simpler – Unique-SAT bounds for PPSZ hold in general - новая нижняя оценка сложности решения 3-SAT - O(1.308ⁿ)

The Grothendieck constant is strictly smaller than Krivine's bound  - Неравенство Гротендика утверждает что если скалярное произведение матрицы A и матрицы B с ограниченными коэффициентами мало, то мало и скалярное произведение матрицы А со всеми матрицами C, которые сформироны как outer product двух единичных векторов. По ссылке, в Википедии это написано пообъемнее и попонятнее. Постоянная Гротендика - это отношение этих двух произведений. Казалось бы, причем тут алгоритмы, но в этом же году вышла другая статья тех же авторов, показывающая связь между постоянной Гротендика и многими задачами комбинаторной оптимизации и вычислительной сложности.

Subexponential parameterized algorithm for minimum fill-in - Задача Minimum Fill-in состоит в том, чтобы определить, можно ли построить триангуляцию графа (плоский граф триангулирован, если к нему нельзя добавить ни одного ребра так, чтобы он остался плоским), добавив к нему не более k ребер. В статье описывается улучшение оценки сложности решения этой задачи с O(2^O(k) + k^2nm) до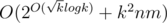

Minimum weight cycles and triangles: equivalences and algorithms - Поиск кратчайшего взвешенного цикла в графе с целыми весами ребер не намного сложнее поиска кратчайшего взвешенного треугольника в более плотном графе с таким же количеством вершин и примерно таким же диапазоном весов. Поскольку мы умеем решать задачу о нахождении треугольников с помощью быстрого перемножения матриц, задача нахождения коротких циклов значительно проще, чем решение задачи APSP

Confluent persistence revisited - Для структур данных можно определить три вида персистентности - частичная (выполнять запросы можно к любой версии, изменять только текущую), полная (в результате изменений предыдущих версий получаем дерево версий) и смыкающаяся - confluent (в результате изменения предыдущих версий получаем DAG). Автор представляет метод эффективного построения confluent persistent структур данных, если в ходе изменений мы не используем две версии одной и той же ячейки структуры при слиянии.

Circle graph recognition in time O(n + m) α(n + m) - Circle graph  - это граф пересечений множества хорд окружности. Новый алгоритм умеет находить множество хорд для данного графа (или определять, что его нельзя представить в таком виде), используя алгоритм для построения лексикографического BFS-упорядочения.

Multiple-source multiple-sink maximum flow in directed planar graphs in near-linear time  - максимальный поток с множеством истоков и стоков обычно сводят к потоку с единственным истоком и стоком. Для планарных графов такое может не работать (если свойство планарности для нас важно, добавлением фиктивных истока и стока мы можем все сломать). Представлен алгоритм, работающий за O(nlog³n).

Counting perfect matchings as fast as Ryser  - В 1963 Райзер показал как считать перманент матрицы (а равно и число полных паросочетаний в двудольном графе с n вершинами) за . Теперь такая же оценка достигнута и для недвудольных графов.

13/9-approximation for graphic TSP - Совсем недавно появилась целая серия работ, улучшающих алгоритм Кристофидеса . Результат исходного алгоритма позволял получить решение в пределах 150% от оптимального. Новый результат снизил эту планку до ~144%.

Надеюсь, при переводе я нигде не допустил серьезных ошибок в терминологии.

Буду рад увидеть замечания/исправления/пожелания в личке.