Для решения этой задачи достаточно посчитать для каждой буквы: ac - количество вхождений буквы c в первые две строки инпута, bc - количество вхождений буквы c в последнюю строку инпута. Ответ на задачу "YES", если для 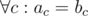 , иначе "NO".
, иначе "NO".
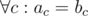 , иначе "NO".
, иначе "NO".Переберем "уровень" 0 ≤ i ≤ 106 , в который предположительно должен попасть камешек, попутно поддерживая наименьший номер квадратика на этом уровне. Далее понимаем, сколько на этом уровне квадратиков один или два. Далее одним или двумя (если на уровне два квадратика) ифами проверяем, попал или нет камешек в соответствующий квадратик, если попал выводим ответ. Если мы не нашли ни одного квадратика, в который попал камешек, выводим "-1".
Отсортируем пары (namei, ai) по возрастанию ai. Если существует такой индекс 0 ≤ i < n, что ai > i, тогда ответ "-1". Иначе ответ существует. Будем идти по массиву отсортированных пар слева направо, поддерживая вектор результата res. Пусть на текущей итерации hi = n - i, тогда текущего человека нужно поставить в текущий вектор на позицию ai. В C++ это можно сделать одной строчкой: res.insert(res.begin() + a[i], man);
Сгенерируем взвешенный ориентированный граф всевозможных переходов. Вершины графа - это важные точки на прямой Ox, т.е. точки 0, L, xi - pi, xi + di. Ребра графа - это возможные переходы, т.е. либо переход из точки xi - pi в точку xi + di, либо переход из вершины в соседние вершины (соседние, в том смысле что мы берем следующую и предыдущую важные точки на прямой). Веса у таких ребер соответственно pi + ti и xv + 1 - xv, xv - xv - 1. В переходах нужно учесть, что нельзя забегать за старт, просто не добавляя такие переходы.
Далее на этом графе нужно найти и вывести кратчайший путь из вершины 0 в L. Это можно сделать, например, алгоритмом Дейкстры для разреженных графов.
Перефразируем условие задачи: нужно найти покрывающее дерево графа, такое что в нем ровно половина ребер помечено буквой S.
В таком дереве всегда будет n - 1 ребро, поэтому если n - четное, ответ "-1".
Давайте удалим из данного нам графа все S-ребра. Пусть теперь в нем будет cnt компонент. Чтобы сделать редуцированный граф вновь связным, нужно добавить минимум cnt - 1 S-ребер, поэтому если cnt - 1 > (n - 1) / 2, ответ "-1". Найдем cnt - 1 S-ребер, которые обязательно придется добавить в граф, чтобы он стал связным, если cnt - 1 < (n - 1) / 2, то будем пытаться добавить в это множество ребер другие S-ребра, так чтобы не получилось цикла по S-ребрам. Все это нужно делать по аналогии с алгоритмом Краскала нахождения минимального по весу остова. Если мы смогли получить множество S-ребер из (n - 1) / 2 элементов, такое что в него входят обязательные cnt - 1 ребер и нет циклов по ребрам, тогда ответ существует. Теперь нужно добавить в это множество (n - 1) / 2 M-ребер так, чтобы получилось покрывающее дерево. Это нужно сделать также по аналогии с алгоритмом Краскала.











кстати, задача Е?
upd: нет, не она
Ну а должен быть ровно один путь, к тому же он должен быть простым. На это третий семпл.
Ну лично я фразу ровно один простой путь. Понимаю как ровно один путь, который должен быть простым. К тому же если бы имело место ваше понимание третий семпл имел бы другой ответ.
1) из всех путей (соединяющих две вершины) ровно один должен быть простым (а значит, мы можем использовать и петли)
2) должен существовать ровно один путь, и он должен быть простым (петли использовать не можем)
Если бы не третий семпл, без клара бы не обошлось однозначно.
По-моему лучше было бы вообще исключить наличие петель из условия и тестов.
Сижу теперь, как дурак с А и С только...
5 -4 2
Вывод
Ответ
спасибо за оперативный разбор
задача Е хорошая, но, имхо, условие не было полноценно понятным
UPD ну вот зачем, зачем добавлять в инпут петли, если их, по условию надо все равно выкидывать?!
Отсортируем пары (namei, ai) по возрастанию ai. Если существует такой индекс 0 ≤ i < n, что ai > i, тогда ответ "-1"
почему, если не выполнилось это условие, не найдется другого варианта построить ответ
Потому что если это выполняется, то для любого a[j] (j>i) это тоже выполняется(если числа в a[] различны), "сдвигать" массив a[] мы тоже не можешь, так как это не улучшит ситуацию.
А если после a[i] идут равные ему, то сдвиг a[i] ничего не изменит.
Пусть на текущей итерации hi = n - i, тогда текущего человека нужно поставить в текущий вектор на позицию ai.
Текущий вектор... Я один ничего не понял? Может кто-то чуть подробнее объяснить как это работает и почему это правильно?
А ведь задача B не только как в разборе перебором решалось, можно было найти решение за константное время =)
Та же история, только моя ошибка всплыла на систестах.
OK, lets do it in English.
Я отсортировал все трамплины по увеличению x+d, затем пока позиция < L проверял, как добраться до точки xi + di быстрее - используя трамплин или без него. Из-за неправильного условия решение не прошло 7 претест. Прошло бы оно системное тестирование?
"Мсье знает толк в извращениях" (с) - это о моем решении задачи D
Ну почему я не догадался построить граф? А вместо этого выдумал какую-то дикую фигню с эмуляцией движения слева направо и с помощью дерева отрезков справа налево. Я раз 5 переписывал решение, причем восстановление пути появилось только в третей версии, когда я наконец нашел ответ :) Прежде чем писать, надо хорошо подумать, это сэкономит время, а не потратит. В B тупой баг - забыл унарный минус. Хорошо хоть раунд для меня нерейтинговый.
That would normally be correct, but here we can have roads that start and end at the same hut, so we can add such a road without changing the connectivity, can't we?
2 2
1 2 S
1 1 M
For this case, isn't the solution to clear both roads?
"between any two huts should exist exactly one simple path along the cleared roads". That case results in 2 paths from 1 to 2. Hence, we can't clear roads which connect the same hut.UPD: I misunderstood it. Your opinion seems correct based on the problem statement.
I think the roads which begin and end in the same hut are useful to adjust one nearly right answer to a right one.
for example, if I got S=10 M=9, and one road 2->2 is M, I can choose this road so that S=M=10.
and the rule above is satisfied, too. because 2->2 is never used, for when it's used nd 2 appeared twice. so whether to choose 2->2 is not important.
To conclude, the solution for problem E is wrong || the problem statement needs change.
все задачи понял, кроме 3. поясните
дураку, что и как... не врубаюсь_ _ _ _ 3
3 - (a[5]+1 == 3-е) число из имеющихся
34 5_ _ _ 4 3
4 - 2-е из оставшихся
345_ _ 2 4 3
2 3 45_ 5 2 4 3
2 3 4 51 5 2 4 3
На С можно было спокойно поставить ограничение 105 - вот решение за nlogn.
UPD. Ошибочка: решение работает за nlogn, я не учел сложность сортировки.
Подскажите пожалуйста, какая итоговая сложность получилась в E, просто я решил совсем по-другому и у меня N^2 + M, и работает оно быстрее всех уже сданных
В решении Е из разбора итоговая сложность как у алгоритма Крускала, т.е. O(m * log(m)), что вполне может работать медленнее Вашего решения.