Представляю разбор Codeforces Beta Round #13. Если будут какие-то вопросы или замечания - прошу писать в комментариях.
Задача A.
Достаточно просто перебрать все основания системы исчисления, просуммировать цифры числа по всем основаниям, а затем найти наибольший общий делитель полученной суммы и числа А-2 (количество оснований систем исчисления) и сократить полученную дробь на найденный НОД. Сложность алгоритма O(A).
Задача B.
Эта задача оказалась довольно неприятной для реализации, но все что нужно было сделать - аккуратно проверить выполнение трех пунктов, данных в условии. В вычислениях рекомендуется использовать целочисленную арифметику, делать все проверки при помощи векторных и скалярных произведений.
Задача C.
Заметим, что существует неубывающая подпоследовательность, которую можно получить из данной за минимальное количество ходов и у которой все элементы равны каким-то элементом начальной последовательности (т.е. в ней встречаются только числа, которые встречались в начальной).
Пусть {ai} - начальная последовательность, а {bi} - она же, только отсортированная и без повторяющихся чисел. Так же пусть f(i,j) - минимальное количество ходов, требуемое для того чтобы из начальной последовательности получить такую, в которой первые i элементов не убывают, причем элемент с номером i не превышает bj. В таком случае ответом на задачу будет f(n,k), где n - количество элементов в {ai}, а k - количество элементов в {bi}. Воспользуемся следующими рекуррентными формулами для вычисления f(i,j):
f(1,1)=|a1-b1|
f(1,j)=min{|a1-bj|,f(1,j-1)}, j>1
f(i,1)=|ai-b1|+f(i-1,1), i>1
f(i,j)=min{f(i,j-1),f(i-1,j)+|ai-bj|}, i>1, j>1
Сложность решения выходит O(N2). Для того чтобы уложиться в ограничение по памяти достаточно заметить, что для вычисления f(i,*) нам достаточно помнить только f(i-1,*) и уже вычисленную часть i-й строки.
Задача D.
Будем решать задачу при помощи такого алгоритма:
- Зафиксируем красную точку.
- Найдем количество треугольников с вершинами в красных точках, которые не содержат в себе синих точек и у которых одна из вершин это зафиксированная в пункте 1 точка.
- Удалим зафиксированную точку из набора и повторим пункт 1, если еще остались красные точки.
Первый и третий пункты пояснения не требуют, поэтому основной частью является пункт 2.
Пусть зафиксирована красная точка А (в первом пункте). Отсортируем все остальные еще не удаленные точки (и красные и синие вместе) по полярному углу относительно А. Затем будем перебирать красную точку B, которая будет второй вершиной треугольника. Теперь нам нужно найти количество треугольников с вершинами в красных точках, причем у которых 2 вершины фиксированы и которые не содержат в себе ни одной синей точки.
Для решения этой задачи, будем перебирать все еще не удаленные точки С в порядке возрастания угла ABC начиная от точки, которая следует за точкой B. Для того чтобы каждый треугольник просмотреть ровно 1 раз, будем останавливаться как только угол между векторами AB и AC станет больше 180 градусов, либо когда мы придем к точке которую уже рассматривали. Будем выполнять такие действия:
- Если C - красная, тогда проверим, есть ли синие точки внутри треугольника ABC и если нет, увеличим ответ на 1. Заметим, что для этой проверки нам не нужно перебирать все синие точки, а достаточно хранить такую синюю точку D из уже просмотренных, для которой угол ABD - наименьший. Если она не принадлежит треугольнику ABC, то никакая синяя точка не может ему принадлежать.
- Если C - синяя, то сравним ее с уже имеющейся D (либо если D еще не найдена, то просто присвоим D=C) и в случае, если угол ABC меньше чем угол ABD, то заменим D на C.
Заметим, что при выборе новой точки B мы считаем что точка D еще не найдена и до тех пор пока не встретится синяя точка считаем что все красные точки образуют с А и B треугольник, не содержащий синих точек.
Сложность алгоритма выходит O(N2(N+M)).
Задача E.
Разделим ряд на блоки длины K=sqrt(N) подряд идущих лунок. Если N не является полным квадратом, то K=sqrt(N), округленное вниз. Для каждой лунки помимо силы ее выброса (power[i]) запомним первую лунку из другого блока, в которую из нее можно попасть при помощи последовательных прыжков (будем считать что за краем ряда находится фиктивная лунка из отдельного блока, в которую мы попадаем при вылете за край из любой лунки) - next[i]. Так же для каждой лунки запомним количество прыжков, требуемое для того чтобы попасть в первую лунку из другого блока - count[i].
Для того чтобы обработать запрос вбрасывания шарика, просто из лунки i будем перепрыгивать сразу в next[i], прибавляя к ответу count[i], пока не придем в фиктивную лунку. Таким образом мы сделаем не более N/K прыжков.
Для обработки запроса изменения силы лунки i, в начале поменяем power[i], count[i] и next[i], а затем для всех лунок из того же блока что и i, которые находятся раньше i в порядке убывания обновим next и count. Таким образом мы сделаем не более K обновлений.
Сложность алгоритма выходит O(Nsqrt(N)).











Пусть красные вершины - R1 ... Rn, синие - B1 ... Bm.
Сначала посчитаем для всех треугольников R1RiRj ориентированное количестово синих точек в нем (т.е. просто количество если R1, Ri, Rj идут по часовой стрелке и количество с минусом если они идут против часовой стрелки) и запишем это число в dp[i][j]. Все это можно сделать за O(N2M) перебрав все i, j и все синие точки и проверив принадлежность за O(1) (*).
Теперь для каждого красного треугольника за O(1) мы можем узнать количество синих точек в нем. Для треугольника RiRjRk будет равно dp[i][j] + dp[j][k] + dp[k][j]. Перебираем все треугольники за O(N3) и считаем ответ.
Итого решение за O(N3 + N2M). Мое решение валилось по времени из-за долгого выполнение (*), хотя асимптотика такая же, как и у авторского решения.
Обидно, что на контесте не прошло... У тебя было N^3 / 6 + MN^2 / 2, да?
Можно было использовать ориентацию, но я вместо этого посортил точки по x-координате и проверял равенство dp[i][k] = dp[i][j] + dp[j][k]. Долго осознавал, что здесь не важно, выше или ниже j-ая точка относительно отрезка. =)
Хорошая задача.
В итоге dp[i][j] = (количество синих точек, лежащих строго под отрезком)*2 + количество синих точек, лежащих под концами. Несложно понять, что это дикое шаманство работает. =)
Но сути проверка под отрезком ли синяя точка в 3 раза быстрее работает чем у меня в треугольнике ли.
Насчет точками под концами отрезков - можно считать, что отрезок на самом деле полуинтервал. Т.е. строго под левым концом отрезка точка лежать может, а под правым нет. Тогда выражение dp[i][k]=dp[i][j]+dp[j][k] работает всегда.
Пришлось минут 15 искать, где соптимизировать (получилось где-то в два раза по времени сэкономить)
В итоге сдал.
Но все-таки тайм лимит явно надо было больше делать, хотя бы 3 секунды.
И еще хотел узнать, как у автора реализован этот этап
"Для того чтобы каждый треугольник просмотреть ровно 1 раз, будем останавливаться как только угол между векторами AB и AC станет больше 180 градусов, либо когда мы придем к точке которую уже рассматривали."
В условии выхода из цикла стоит проверка на векторное произведение, или методом двух указателей поддерживается номер вершины, до которой нам надо идти?
Потому что я как раз переделал с первого способа на второй, и тогда оно прошло.
Я умею ее решать словами Linking-Cutting trees за O(Nlog^2N) и O(NlogN). Долго понимал, чем эта задача принципиально легче чем структура Linking-Cutting trees в общем случае. Структуру, кстати, никогда не писал и давно хотел попробовать... Минут за 30-40 вроде пишется... Ели поборол искушение :)
Подумал, что тесты дурацкие. Написал эвристику, которая часто за O(Nlog^2N) работает. Хорошие тесты. Respect.
А под конец контеста все стер и за 7 минут с нуля закодил корневую эвристику. Nsqrt(N). Accepted=)
Круть. Первая задача, которую я не умею без корневой эвристики решать каким-нибудь простым деревом.
Кто умеет, поделитесь, пожалуйста. Ищу решения быстрее чем O(Nsqrt(N)) :)
Структура называется Euler-Tour tree (храним в любом сбалансированном дереве с операциями Split и Merge Эйлеров обход дерева). Если ты ее придумал сам и на контесте, здорово ;-)
С помощью нее, кстати, (недавно изучал, вспомнилось) решается задачка Dynamic Connectivity Problem: есть граф, можно добавлять и удалять ребра, нужно отвечать на запрос "лежат ли a и b в одной компоненте связности".
Разные таблицы прыжков на 2^k вперед, которые иногда лениво пересчитывались (естественно, не всегда и не целиком).
У меня зашло за O(Nlog^2N). Идея в том, что мы выбираем половину изменений, находим какие вершины они меняют. Делаем сжатие путей так, чтобы все прыжки вели в изменяемые вершины (и при этом всегда вели в первую изменяемую вершину на пути). После чего решаем задачу на изменяемых вершинах. Там тоже делим количество изменений пополам и.т.д. Квадрат логарифма вылезает из-за того, что после обработки изменений в рекурсивных вызовах, мне нужно "разжать" пути обратно. Таким образом я поддерживаю инвариант, что текущие сжатые дуги указывают на первую вершину в пути, которая попадает в текущее подмножество вершин. Для этого я после обработки изменений в рекурсивных вызовах просто рассчитываю все сжатые дуги для текущего подмножества заново за O(NlogN). Наверное это доводится до O(NlogN), но нужно реализовывать как-то аккуратнее.
Ссылка на решение: http://mirror.codeforces.com/contest/13/submission/13762281
"Заметим, что существует неубывающая подпоследовательность, которую можно получить из данной за минимальное количество ходов и у которой все элементы равны каким-то элементом начальной последовательности (т.е. в ней встречаются только числа, которые встречались в начальной)."
Как это можно доказать? ну или хоть как то идею доказательства понять?
There is another way to solve problem D. You can count the amount of points (x, y) below each segment (ax, ay) - (bx, by) with ax ≤ bx such that ax < x ≤ bx in O(N2M) and store these values in a table. Then you can compute the result by iterating over all triangles and counting the points inside the triangle in O(1) using the values stored in this table.
About Problem C.
f(1,1)=|a1-b1|
But i think following statement is not true.Do you agree with me?
Let f(i,j) be the minimal number of moves required to obtain the sequence in which the first i elements are non-decreasing and i-th element is equal to bj
I think it must be like that:f(i,j) is the minimal number of moves required to obtain the sequence in which the first i elements are non-decreasing and i-th element is at most bj.(can be equal to any of bk, while k=1,2,...,j-1,j)
Note that:
f(i,j)=min{f(i,j-1),f(i-1,j)+|ai-bj|}, i>1, j>1.
In Problem E: lets save for each hole the answer , number of jumps after ball leaves this hole and the last hole for it. Then for each query we have answer in o(1) and for each update of strength we can look the hole which will be after this hole . ((new strength)+i) and rewrite its answer to this hole and increase the first answer (number of jumps ) by 1 and second answer (last hole) will be same. This is o(M) solution . Any mistake ?
Do you really think that problem E can be that easy? After updating the strength of the hole number X the answer will change not only for the hole X, but also for all holes Yi from which X is reachable by 1 or more jumps. The number of such holes Yi is O(N).
Problem C :in which all elements are equal to some element from the initial sequence
Why? to get the min step , the final sequence 's every number is same to the initial sequence?? why is this optimal? Thanks.
Well, to be more precise, we can say that there IS an optimal final sequence whose numbers are all from the original sequence, which can be proved by contradiction. Take the original sequence "3 1" for example. Although "2 2" is an optimal one whose numbers are not from the original sequence, "1 1" or "3 3" is optimal and their numbers are from the original one.
kadar not able to visualize the solution can you please help me do that ?
Can someone please give me a good link for square root decomposition.
i found various links on google but don't know which one is good and contains all details on sqrt decomposition.
https://cp-algorithms.com/data_structures/sqrt_decomposition.html
Problem E can also be solved using the Link-cut tree in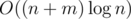 .
.
Anyone noticed that Problem E also required the number of the last hole the ball visited?
So we'll have to jump to the block before we jump to the fictious hole and jump to the last hole before we jump to the fictious hole. So I had to add another while loop.
But it seems that the complexity is the same? Well, I'm just here to say that the type 1 query is not that easy(probably still easy for great coder,but not for this noob)
And I've got a TLE on test 13.Anyone help me?
I am also facing a similar issue, please help TLE at test case 13.
278983183
solve C
In problem E,
but also the number of the first hole which belongs to other, do the number here refer to the smallest index of hole in which are residing in different segment and also could be hopped on through a series of jump ?I did E using square root decomposition (Divided the array into blocks of size sqrt(n), then for each element stored only the last index within its block after which it jumps to an element in another block or out of the array).
My O(n * sqrt(n)) solution is getting TLE on testcase 16. Can anyone help? 285297411
I'm getting a Wrong Answer (WA) on test case 3 while using Square Root Decomposition. Can anyone help me figure out why? For the problem E **** //
include<bits/stdc++.h>
define ll long long
define endl "\n"
using namespace std;
vector<map<ll, pair<ll, ll>>> mp; ll flg[100005]; ll arr[100005]; ll n, k; vector<pair<ll,ll>>combi;
void findd() { ll l; cin >> l; ll val = 0; while (1) { ll com = flg[l]; val += mp[com][l].second; if (mp[com][l].first == l || com == 0) { cout << mp[com][l].first << " " << val << endl; break; } else l = mp[com][l].first; } }
void update(ll i) { ll e = combi[i].first; ll s = combi[i].second; map<ll, pair<ll, ll>> mm; for (ll j = e; j >= s; j--) { ll p = arr[j] + j; if (p > n) p = j; mm[j] = {p, 0}; if (flg[j] == flg[p]) { mm[j].second = mm[p].second + 1; mm[j].first = mm[p].first; } else mm[j].second = 1; } mp[i] = mm; }
void out() { ll i=0; for (auto v : mp) { cout<<"block "<<i<<endl;i++; for (auto p : v) { cout << p.first << " = " << p.second.first << " " << p.second.second << endl; } cout << endl; } }
int main () { ios_base::sync_with_stdio(0); cin.tie(0); cin >> n >> k; for (ll i = 1; i <= n; i++) cin >> arr[i]; ll x = sqrt(n); mp.resize(x+2); ll cnt = 0; ll s = 0; pair<ll,ll>pp; for (ll i = n; i > 0; i--) { if(cnt==0)pp.first=i; cnt++; flg[i] = s; if (cnt == x || i==1) {pp.second=i;combi.push_back(pp); cnt = 0; s++; } }
// update all from end; for(ll i=0;i<combi.size();i++) update(i); for (ll i = 0; i < k; i++) { ll t; cin >> t; if (t == 1) findd(); else if (t == 0) { ll i; cin >> i >> arr[i]; update(flg[i]); //out(); } }} // ****