Только что закончилась заочка на olympiads.ru. Предлагаю здесь обсуждать ее. Лично меня интересует решение задачи J.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
30:09:45
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
30:09:45
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 11:25:16 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Я думал, что там триангуляция Делоне + построение минимального остовного дерева с ее использованием...Но реализовать не успел
UPD я почти уверен, что есть решения попроще, расскажите кто-нибудь, плиз
Решение за N^5 очевидно. Перебираем три точки к которым крепится изумруд, и строим за N^2 минимальный остов. За 2 секунды такое не прокатит, надо как-то соптимизировать этот процесс. По сути каждый тест добавляет к множеству рёбер еще три ребра
нулевойнекоторой стоимости (хотя можно сделать её и нулевой), и нужно проделать поряка N^3 / 6 таких посиков минимального остова. Вроде что-то чувствуется такое, но не могу сообразить.Можно ещё проще!
Просто гуглим "координаты точки Ферма/Торричелли/Штайнера" и смотрим первые несколько ссылок. Хотя, вообще говоря, формулы страшные.
Мне выкинуло вот это.
если уж на то пошло-гуглить, то хоть точку ферма надо найти самому для приличия, а то задача полностью превращается баян несусветный (на 60)
На самом деле достаточно просто. Надо найти количество полных подграфов величины 1, 2, 3 и 4 в почти полном графе. Количество полных подграфов величины 1, 2 и 3 ищется понятно как. Для того чтобы искать количество подграфов величины 4 будем перебирать две первые вершины (назовем их i1 и i2, и конечно они должны быть совместимы). Добавим к ответу для каждой такой пары количество таких пар i3 и i4, что i1<i2<i3<i4 а также i1 совместима с i3 и i4 и i2 тоже совместима с i3 и i4. Мы получим ответ, в котором не учтен случай, когда четверка подходит под условие выше, однако i3 и i4 несовместимы. Понятно, что в таком случае будет K таких "плохих" пар (i3, i4), т.е. это будут ребра данные во вводе. Переберем каждое ребро и для него посчитаем количество таких пар (i1, i2), которые будут совместимы с (i3, i4), причем (i1, i2) не является ребром и отнимем это количество от ответа. Ну, вообще это сложно нормально объяснить. Код.
2) Три ребра, имеющие общую вершину
Есть онлайновое решение. Последовательно добавляя ребра (u, v), будем на каждое ребро будем считать, сколько сочетаний, которые могли пойти в ответ, исключаются текущим ребром. При этом поддерживаем граф списками смежности и компоненты смежности графа в DSU, считая для каждой компоненты колличество её вершин и рёбер.
Для сочетаний длиной 1 и 2, решение, понятно, за константу. Для сочетаний длиной 3 ответом будет n - 2 - (g[u].size() + g[v].size()) + пересечение g[u] и g[v].
Для 4 нужно подсчитать все пары вершин, которые не содержат u, v, и их соседей, между которыми нет ребра.
Но это решение скорее нужно отнести к шаманству, наверняка есть более простое решение.
UPD: реализация.
Можно вообще без LCA почти также. См ниже
Не уверен, что правильно но 60 получает.
Очевидно, искомая точка находится в т. Торричелли какого-то треугольника или ее вообще быть не должно. Докажем, что ребра, не входящие в минимально остовное дерево для начального графа(без добавленной точки), никогда не войдут в ответ.
Возьмем простой цикл. Самое большое ребро этого цикла никогда не будет ребром никакого остовного дерева, выкинем его. В конце концов, останется дерево. Других ребер быть не должно.
Пусть d[i][j] - max ребро на пути из i в j. Это легко насчитывается за куб. Теперь переберем все треугольники. У нас есть n + 2 ребра, нужно научиться выкидывать 2 ребра за константу. Рассмотрим этот треугольник (i, j, w). Есть всего 3 кандидата: d[i][j], d[i][w], d[j][w]. Если аккуратно посмотреть на эту конструкцию, легко доказать, что среди этих трех присутствуют 2 одинаковых ребра. Их и выкинем. В итоге О(N^3).
Из трех ребер d[i][j], d[i][w], d[j][w] есть 2 одинаковых. То, что они все не равны тоже доказывается.
Короче, если их положить в сет, размера сета равен 2.
Строим в самом начале минимальное остовное дерево. Теперь за куб перебираем тройки (A, B, C), для них находим точку ферма, и теперь дфсом пытаемся найти два таких ребра(наибольшего веса, и не ребра, соединяющие точку ферма с точками A, B, C), чтобы граф сохранял связность и был деревом. Очевидно, что эти ребра будут лежать на путях между вершинами(A, B, C). Сложность O(n^4 / 6).
К сожалению идея пришла в последний день, закодить так и не получилось =(
Пробовал, у меня WA на 5-ти тестах.
а я нагуглил барицентрические координаты точки Ферма :)
а именно: BC/sin(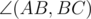 + pi / 3) ...
+ pi / 3) ...
Я буду читать номер задачи, перед тем как отвечать.
Я буду читать номер задачи, перед тем как отвечать.
Я буду читать номер задачи, перед тем как отвечать.
Скажите, пожалуйста, почему у меня вылетало 6 тестов. Задача E количество кратчайших путей.
Кстати, решение без длинной арифметики падало на пяти последних тестах.
Решение за константу для задачи про фибоначчи, когда k < i?
Используя формулу a[j] = fib(j - i - 1) * a[i] + fib(j - i) * a[i + 1],где fib(x) - х-тое число фиббоначи, находим i + 1 элемент последовательности. Потом считаем назад числа в порядке уменьшения, пока не получим число под номером k.
У меня все промежуточные вычисления в long long'ах, решение за O(1). Стоит 100.